Hoe vaak woorden voorkomen berust niet op toeval, maar volgt een sterke wetmatigheid. Deze staat bekend als de Wet van Zipf. Hoewel meerdere studies dit patroon in taal hebben aangetoond, was tot nu toe geen sluitende verklaring aangedragen voor het fenomeen. Taalwetenschapper Sander Lestrade van de Radboud Universiteit toont in een recente studie aan hoe de vork in de steel zit.
Als je een willekeurig Nederlands boek openslaat, welk woord komt dan het meest voor? Dat is waarschijnlijk het woordje ‘de’. Ook ‘van’ en ‘het’ scoren hoog in frequentie. Hoe vaak we een woord gebruiken, verschilt nogal: een lidwoord komt voor in vrijwel iedere uiting, maar een doorsnee zelfstandig naamwoord als ‘vlindertuin’ praktisch nooit. Dat we het ene woord vaker gebruiken dan het andere, is geen toeval.
Zowel de woordklasse waar een woord toe behoort (lidwoord, werkwoord, zelfstandig naamwoord, et cetera) als de betekenis spelen hierin een belangrijke rol. Dat toont Sander Lestrade aan in een recent artikel in PLOS ONE. Hij ontwikkelt al jaren computermodellen die taalevolutie simuleren. “Daarbij zag ik steeds weer Zipfiaanse patronen ontstaan”, vertelt de onderzoeker. “De wet van Zipf speelt een belangrijke rol binnen de computationele taalkunde. Onderzoekers hebben op allerlei manieren geprobeerd deze te verklaren, soms zelfs door apen op toetsenborden los te laten, maar tot nu toe zonder succes.”
Wet van Zipf
De wet is vernoemd naar de Amerikaanse filosoof en taalkundige George Kingsley Zipf. Hij deed begin vorige eeuw al onderzoek naar woordfrequentie in verschillende talen. Zipf ontdekte een patroon in de woordfrequenties, dat uitgedrukt kon worden in een simpele formule. Het meest voorkomende woord, in het Nederlands ‘de’, komt namelijk twee keer zo vaak voor als het op één na meest voorkomende woord, in het Nederlands ‘van’, en drie keer zo vaak als het derde meest voorkomende woord, in het Nederlands ‘het’, et cetera, tot aan het minst gebruikte woord in de tekst. In een formule gevat: de rang van een woord r maal de frequentie van een woord f is constant. Dit werd de wet van Zipf.
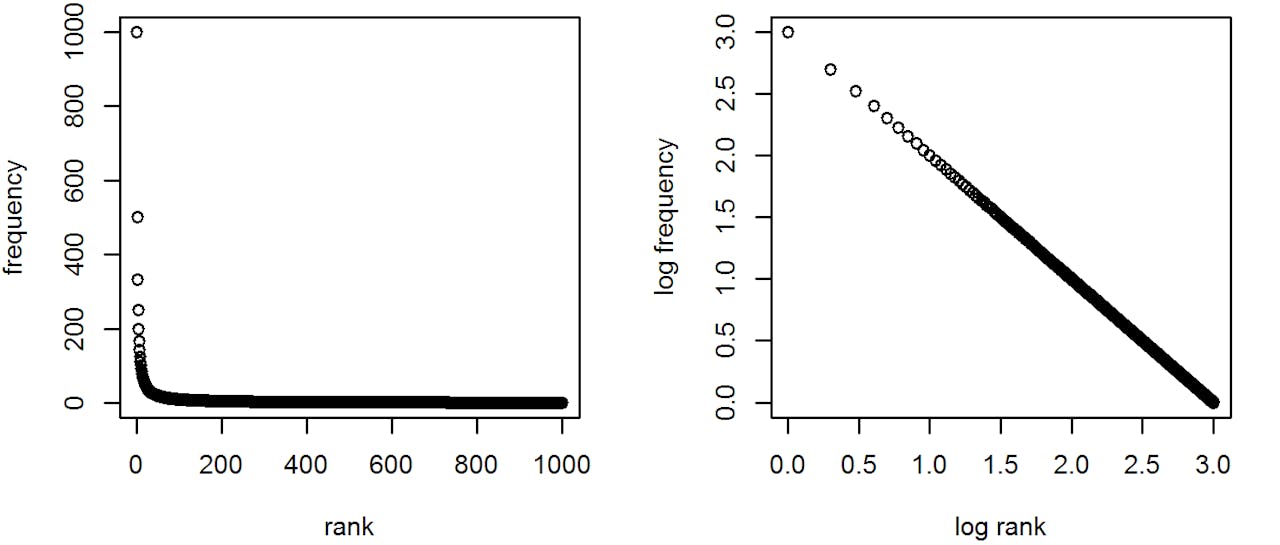
De hockeystick-vorm (plaatje 1) is kenmerkend voor de Zipfiaanse verdeling. Als je deze in een dubbellogaritmische grafiek zet, krijg je een perfecte rechte lijn met een richtingscoëfficient van -1 (plaatje 2).
2017 Sander Lestrade, PLOSToch was Zipf niet de eerste wetenschapper die dit patroon ontdekte, vertelt Lestrade. “Ook andere onderzoekers hadden al een dergelijk patroon gevonden voor woordfrequentie. Zipf was wel de eerste die er een verklaring voor probeerde te geven, maar die was nogal algemeen en moeilijk te controleren. Hij wijdde het verschijnsel aan het Principle of Least Effort, wat voor de spreker inhoudt dat hij het liefst altijd hetzelfde woord gebruikt – dat scheelt zoeken naar het juiste woord – en voor de hoorder dat hij het liefst een specifiek woord voor iedere betekenis krijgt – dat scheelt zoeken naar de juiste betekenis.”
Fundamenteel
Er zijn tientallen verklaringen voorgesteld voor de wet van Zipf, maar geen enkele is bevredigend. Zonder verklaring was de wet evengoed bruikbaar voor allerlei computersimulaties. Lestrade vergelijkt het met de wet van Newton: “Ook voordat mensen kennis hadden van de achterliggende theorie voor de zwaartekracht waren ze in staat om tafels te bouwen zodat hun eten niet op de grond viel.”
Een praktische noodzaak voor het verklaren van de wet van Zipf was er dus niet. Maar het geeft ons wel een fundamenteel inzicht in ons taalsysteem. In zijn artikel toont Lestrade eerst aan hoe belangrijk woordklasse is voor de wet van Zipf. “In elke taal is de grootte van woordklassen enorm verschillend. Het grootste verschil is dat tussen lidwoorden en zelfstandig naamwoorden. Van lidwoorden zijn er nooit meer dan een handjevol, zoals in het Nederlands ‘de’, ‘het’ en ‘een’. Die komen dan ook vaker voor dan een willekeurig zelfstandig naamwoord, want daarvan zijn er tienduizenden. Het is een zogeheten open woordklasse: er komen steeds weer nieuwe bij.”
Daarentegen komen alle woordklassen ongeveer even vaak in een tekst voor. Zo is in het Nederlands 6 procent van de woorden een lidwoord, 17 procent een werkwoord, en 13 procent een zelfstandig naamwoord. Dit loopt dus veel minder uiteen dan de groottes van de woordklassen. Alleen al dit feit, en de onrealistische aanname dat elk woord in een woordklasse even vaak gebruikt wordt (‘de’ even vaak als ‘het’; ‘spinazie’ even vaak als ‘moersleutel’) levert een ruwe benadering van de wet van Zipf op. Maar om een goede overeenstemming met de wet van Zipf te krijgen, is nog een ingrediënt nodig, en die is te vinden in de woordbetekenis. Lestrade: “Waarom komt het lidwoord ‘de’ vaker voor dan het lidwoord ‘het’? Dat komt doordat je ‘de’ zowel voor enkelvoud als meervoud kunt gebruiken, zoals in ‘de man’ en ‘de mannen’. In meerdere betekenissen dus. Ook een algemener woord zoals ‘ding’ komt vaker voor dan een meer gespecificeerd woord zoals ‘onderzeeboot’.”
Hockeystick
Lestrade maakte een computermodel dat simuleert hoe woorden uiteenlopen in de algemeenheid van hun betekenis, en wat dat betekent voor de kans dat een woord in die woordklasse gebruikt wordt in een tekst. In plaats van de simplistische aanname dat elk woord in een woordklasse even vaak gebruikt wordt, komt dus een meer subtiele frequentieverdeling per woordklasse.
Met dit ingrediënt erbij ontstaat de specifieke hockeystick-vorm die kenmerkend is voor de Zipfiaanse verdeling. Als je de Zipfiaanse verdeling in een dubbellogaritmische grafiek zet, krijg je een perfecte rechte lijn met een richtingscoëfficient van -1. De woordfrequenties van echte teksten wijken daar een klein beetje van af. “Het mooie aan mijn resultaten is dat ze net zo afwijken van deze rechte lijn als natuurlijke taal”, vertelt Lestrade. “Bovendien verschillen woordklassen per taal, en dat zorgt voor verschillen in de verdeling.”
Universele wetmatigheid
De wet van Zipf is aangetoond voor allerlei verschillende talen. Maar ook van niet-taalkundige fenomenen, zoals inwoneraantallen van steden in de Verenigde Staten, wetenschappelijke productiviteit, of aantallen bezoekers van websites wordt soms gezegd dat zij voldoen aan de wet van Zipf. Om die reden is er veel getheoretiseerd over een verborgen, universele wetmatigheid achter de wet. Maar de overeenkomst is slechts globaal, ze wijken er allemaal op hun eigen manier van af: óf ze hebben een compleet andere richtingscoëfficiënt, óf ze gedragen zich alleen in het begin netjes, maar ‘breken’ na een tijdje.
Verder voldoet een machtsfunctie, om puur wiskundige redenen, al gauw ongeveer aan de wet van Zipf als je niet de groottes zelf (woordfrequentie, inwoners van een stad, bezoekcijfers van een website) in een grafiek uitzet, maar hun rangorde: dus ‘grootste’, ‘één na grootste’, enzovoort. Door de manier waarop de informatie ‘op een rijtje’ gezet wordt, is het niet heel verrassend dat uiteenlopende fenomenen aan ongeveer dezelfde ‘wet’ voldoen.
Om te voldoen aan de wet van Zipf, is dus een taalspecifieke verklaring nodig, waarbij de juiste ingrediënten gecombineerd worden.

