In medisch onderzoek vinden we het fijn om heel veel mensen te bestuderen. Als we willen weten of cholesterolverlagers het risico op hartaanvallen verminderen, of overgewicht leidt tot nierschade, geldt vanuit epidemiologisch perspectief: “hoe meer mensen, hoe beter.” Waarom is dat eigenlijk zo?
In medisch onderzoek willen we graag zo veel mogelijk mensen bestuderen. Dit heeft alles te maken met de invloed van toeval op de resultaten van ons onderzoek. Aan middelbare scholieren van het Pre-University College in Leiden leggen we de rol van toeval uit met het volgende voorbeeld:
Stel je voor dat je wil weten wat de gemiddelde lengte is van de 5-VWO scholier in Nederland. Volgens het CBS waren er in Nederland in het jaar 2018-2019 44.631 middelbare scholieren die in de vijfde klas van het VWO zitten).

Hoe meet je hoe lang scholieren uit 5-VWO zijn?
Pixabay CC0Om achter de gemiddelde lengte te komen kan je elk van die 44.631 scholieren opmeten, maar dat kost veel te veel tijd en geld. In plaats van al die scholieren te meten, nemen we daarom een zogeheten steekproef van tien personen. Dit betekent dat we willekeurig tien scholieren nemen die in 5-VWO zitten. Van die tien scholieren meten we dan de lengte en berekenen we het gemiddelde.
Stel je nu eens voor dat we in een perfect universum leefden en daarom wisten dat de werkelijke gemiddelde lengte van de 5-VWO scholier precies 170 cm was. Komt uit onze steekproef van tien scholieren dan ook 170 cm?
Waarschijnlijk niet. Puur op basis van toeval kan er een heel lang persoon in onze steekproef zitten, die het gemiddelde omhoog trekt, bijvoorbeeld naar 175 cm. Of misschien zit er toevallig wel een wat kleiner persoon in onze steekproef, waardoor het gemiddelde 166 cm wordt. Het onderstaande plaatje laat mooi zien wat er gebeurt als we niet een, maar 1000 steekproeven zouden nemen (dus we herhalen ons onderzoekje van 10 scholieren duizend maal).
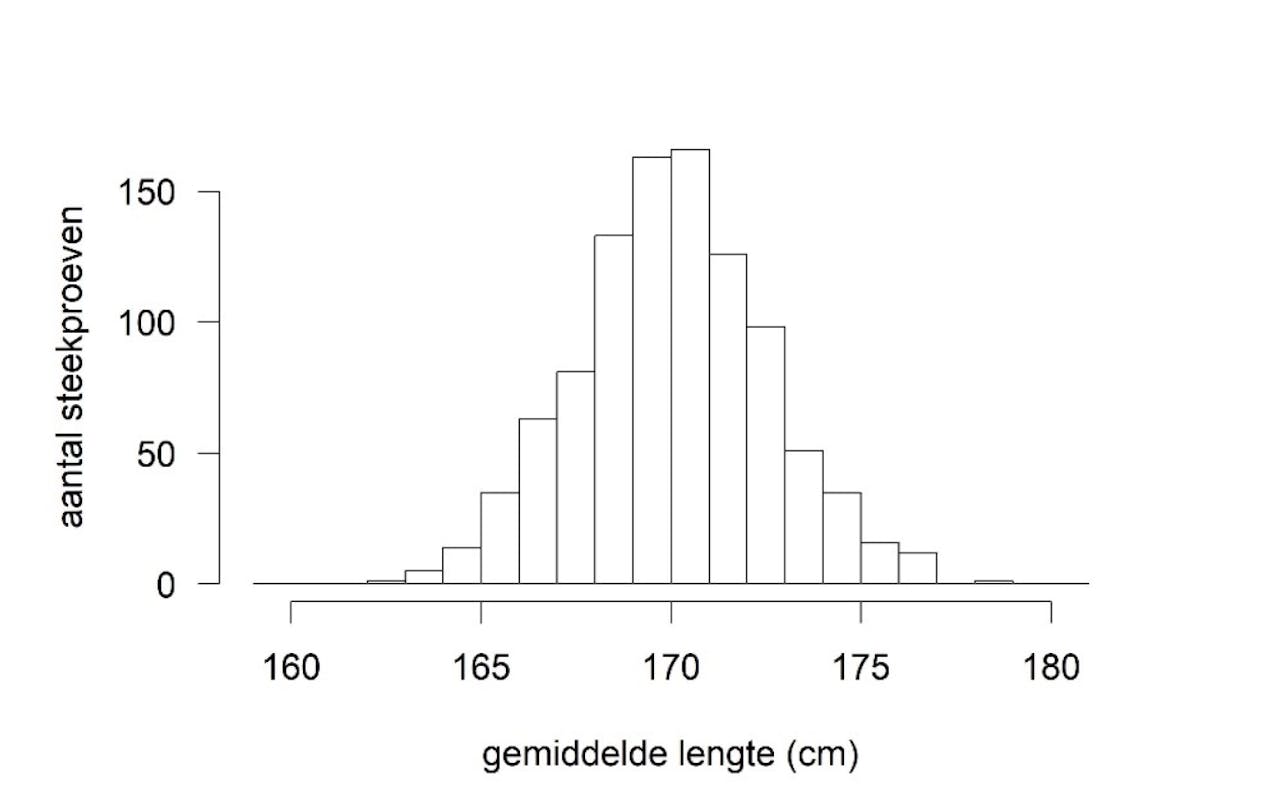
In dit experiment zijn 1000 steekproeven gedaan met in elke steekproef tien scholieren. Voor elke steekproef is de gemiddelde lengte berekend. Op de horizontale as staat de gemiddelde lengte die is gevonden en op de verticale as het aantal steekproeven dat deze lengte vond. De werkelijke gemiddelde lengte is 170 cm. De meeste steekproeven liggen tussen 165 en 175 cm. Figuur ontleend aan Prof. Rolf Groenwold.
Figuur ontleend aan prof. Rolf GroenwoldOp de horizontale as staat de gemiddelde lengte, en op de verticale as staat het aantal steekproeven dat die bepaalde lengte vindt. Wat je ziet is dat de meeste steekproeven tussen de 165 en 175 cm liggen, en dat het gemiddelde van alle steekproeven 170 cm is. Dit plaatje illustreert precies de rol die toeval speelt in medisch onderzoek. Het is namelijk helemaal niet gek om in een enkele steekproef een gemiddelde lengte van 166 cm te vinden, terwijl het gemiddelde van alle scholieren in werkelijkheid 170 cm is.
Hoe meer, hoe beter
Stel je nu eens voor dat we niet tien mensen in onze steekproef nemen, maar 1000 mensen. Er kunnen dan wat lange mensen in de steekproef zitten, en wat korte mensen. De kans is echter bijzonder klein dat we in onze steekproef van wel duizend mensen een gemiddelde lengte van 165 cm vinden, terwijl die in wekelijkheid 170 cm was. Omdat we zoveel mensen hebben, middelen lange en korte mensen elkaar wel uit.
Oftewel, hoe meer mensen we in onze steekproef stoppen, hoe kleiner de rol van toeval is, en hoe zekerder we zijn van ons resultaat.

Hoe meer mensen we in onze steekproef stoppen, hoe kleiner de rol van toeval is
Pixabay CC0Dat zie je terug in het onderstaande plaatje, waar op de horizontale as weer de gemiddelde lengte staat, en op de verticale as het aantal steekproeven dat die bepaalde lengte vindt. We hebben weer duizend steekproeven gedaan, maar ditmaal van duizend scholieren, en zien nu dat alle steekproeven tussen 169 en 171 cm liggen! Hoe groter onze steekproef, hoe dichter onze berekening bij de werkelijke lengte ligt.
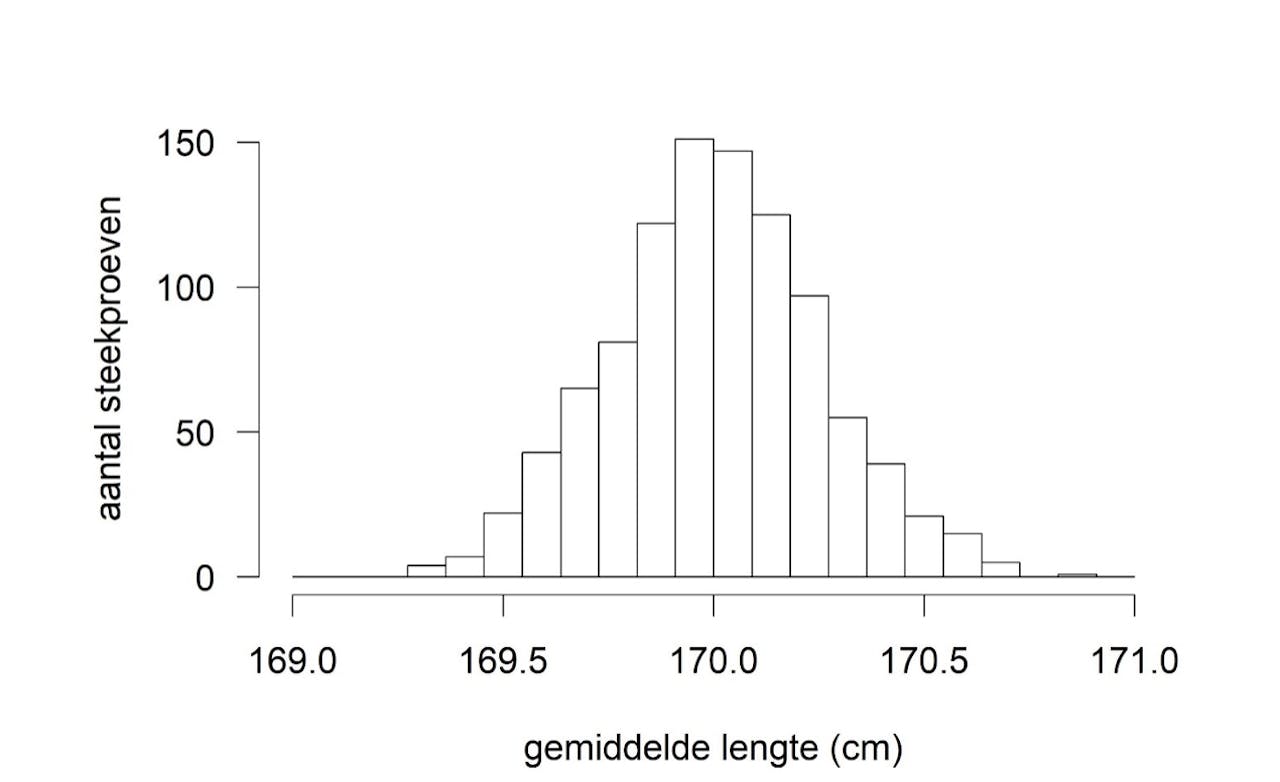
In dit experiment zijn 1000 steekproeven gedaan met in elke steekproef 1000 scholieren. Voor elke steekproef is de gemiddelde lengte berekend. Op de horizontale as staat de gemiddelde lengte die is gevonden en op de verticale as het aantal steekproeven dat deze lengte vond. De werkelijke gemiddelde lengte is 170 cm. De meeste steekproeven liggen nu tussen 169.5 en 170.5 cm, dus veel dichter bij de werkelijke waarde dan in het experiment van 1000 steekproeven met maar 10 scholieren. Figuur ontleend aan Prof. Rolf Groenwold.
Figuur ontleend aan prof. Rolf GroenwoldMaar wacht eens even: in je vorige voorbeeld leefde je in een perfect universum en wist je van tevoren al wat de gemiddelde lengte was, namelijk 170 cm. Maar wat als we niet de werkelijke gemiddelde lengte weten? Kunnen we die dan schatten aan de hand van onze steekproef?
Hoe lang zijn we?
De discipline die zich hiermee bezig houdt heet de statistiek. Met behulp van de principes van de statistiek en onze steekproef kunnen we namelijk berekenen wat de werkelijke waarde ongeveer is. Dit doen we door een zogeheten betrouwbaarheidsinterval te berekenen. Het betrouwbaarheidsinterval geeft, informeel gezegd, een serie van mogelijke waarden. Oftewel, gegeven wat ik heb gevonden in mijn steekproef, wat zou dan de werkelijke waarde kunnen zijn? 1
Laten we zeggen dat we in ons onderzoekje van tien scholieren een gemiddelde van 169,8 cm vonden. Als we hier een betrouwbaarheidsinterval bij berekenen, dan zou het betrouwbaarheidsinterval in dit geval van 164,8 tot 174,8 lopen.
We zijn er dan vrij zeker van dat de werkelijke waarde tussen 163,6 en 173,6 cm ligt. Stel nu dat we hetzelfde gemiddelde in onze steekproef van duizend scholieren vinden. Het betrouwbaarheidsinterval wordt dan een stukje kleiner; hij loopt nu nog maar van 169,6 tot 170,1 cm. We kunnen nu dus met een veel grotere precisie vertellen tussen welke waarden we verwachten de echte lengte te vinden! Wat je hier ziet is dat het betrouwbaarheidsinterval kleiner wordt naarmate de steekproef groter wordt (163,6-173,6 bij een steekproef van 10 mensen tegenover 169,6-170,1 bij een steekproef van 1000 mensen). Hoe groter de steekproef, hoe kleiner de rol van toeval, en hoe zekerder we zijn van ons resultaat.
Toeval is niet alles in medisch onderzoek
Toeval is echter niet alles in medisch onderzoek, en er zijn twee kanttekeningen die ik bij dit verhaal moet plaatsen. Ten eerste moet ik iets vertellen over bias. Het is inderdaad waar dat hoe groter het onderzoek, hoe kleiner de invloed van toeval. Dus hoe meer mensen, hoe beter. Maar dat hoeft absoluut niet te betekenen dat het resultaat van ons onderzoek correct is, oftewel dat ons resultaat dicht bij de waarheid ligt.
Stel je namelijk nu eens voor dat het meetlint dat we gebruikten om de scholieren op te meten was afgescheurd, en pas begon te meten vanaf 20 centimeter. En stel dat we nu tienduizend scholieren hadden opgemeten. Dat betekent dat de gemiddelde lengte ongeveer 190 cm zal zijn, met een heel klein betrouwbaarheidsinterval. De rol van toeval is zeer klein, wat zich uit in het kleine betrouwbaarheidsinterval.
Toch is het resultaat dat we vinden, 190 cm, incorrect. In epidemiologische termen noemen we dat ook wel bias. Zeker nu we steeds meer gebruik maken van routinematig verzamelde “big data”, speelt toeval een kleinere rol, maar wordt de bias wel steeds belangrijker. Grote onderzoeken zijn dus niet per definitie beter dan kleine onderzoeken.
De tweede kanttekening is dat we ook weer niet te veel mensen mee willen laten doen aan een medisch onderzoek. Meer deelnemers kosten niet alleen meer geld en meer tijd om het onderzoek uit te voeren (en veel onderzoek wordt deels uit belastinggeld betaald), maar heeft ook ethische bezwaren. Onderzoek is belastend en niet zonder risico’s. We willen dus niet meer mensen mee laten doen dan strikt noodzakelijk. Bij medische onderzoeken wordt daarom vaak een zogeheten powerberekening gedaan, waarbij wordt berekend hoe groot de steekproef moet zijn om het effect van een medische behandeling aan te kunnen tonen. En dit alles vanwege de rol van toeval!
Deze blog is gebaseerd op een college van Prof. Rolf Groenwold van 10 februari 2020 aan Pre-University College studenten aan de Universiteit Leiden.
1 De formelere definitie van een zogeheten “95% betrouwbaarheidsinterval” is dat als we ons onderzoek honderd keer zouden herhalen, dat dan bij 95 van de 100 steekproeven de werkelijke waarde binnen het betrouwbaarheidsinterval ligt. Stel dat de werkelijke waarde 170 cm is. Bij herhaaldelijk onderzoek zal die 170 cm bij 95 van de 100 steekproeven binnen het betrouwbaarheidsinterval vallen. Je berekent een betrouwbaarheidsinterval aan de hand van de grootte van de steekproef en de spreiding van de data (hoe ver liggen de lengtes van de steekproef uit elkaar). Hoe groter de steekproef en hoe kleiner de spreiding, hoe kleiner het betrouwbaarheidsinterval.

