Natuurkundig probleem blijkt principieel onbeslisbaar en biedt daarmee nieuwe mogelijkheden voor toepassingen in de nanotechnologie

Dankzij het werk van Kurt Gödel en Alan Turing, is al sinds de jaren 30 bekend dat sommige wiskundige stellingen onbeslisbaar zijn; gegeven de gangbare spelregels van de wiskunde is zo’n stelling noch waar, noch onwaar. Voor het eerst is nu van een natuurkundig probleem aangetoond, dat dit onbeslisbaar is. Dat is geen fiasco voor de natuurkunde, het opent juist fascinerende nieuwe mogelijkheden.

28 december 2015

“Dit is cool, zeg!” Na een snelle scan van het artikel in Nature is theoretisch fysicus Jan Zaanen meteen enthousiast over dit kunststukje van drie wiskundigen. “Ik kan weliswaar de details niet controleren, maar ik heb er alle vertrouwen in dat het technisch gezien klopt.” Zaanen en zijn collega’s aan het instituut Lorentz van de Universteit Leiden rekenen vaak aan quantum-veeldeeltjessystemen. Dat is het type systeem waarover de wiskundigen Toby Cubitt, David Perez-Garcia en Michael Wolf in Nature schrijven.

Zich met elkaar bemoeien

Maar wat is een quantum-veeldeeltjessysteem? Daarvoor moeten we naar de quantummechanica. Elk brokje materie, of het nu een stuk metaal, een steen of een vloeistof is, bestaat uit heel veel atomen, en op elk atoom zijn de wetten van de quantummechanica van toepassing. Bovendien bemoeien die atomen zich allemaal met elkaar, ze oefenen bijvoorbeeld krachten uit op hun naaste buren. Elk brokje materie is daarom een quantum-veeldeeltjessysteem.

Je kunt in een wiskundige vergelijking weergeven hoe hard elk lid van een quantum-veeldeeltjessysteem aan zijn naaste buren trekt of er tegenaan duwt. Uit al dat duwen of trekken door individuele deeltjes ontstaat collectief gedrag van het systeem als geheel.

Iets dergelijks zie je gebeuren in mensenmenigtes. Als er fysiek geduwd en getrokken wordt, kan de menigte als geheel op drift raken, terwijl je daar als individu geen controle meer over hebt. Maar het duwen en trekken kan ook figuurlijk zijn, bijvoorbeeld als iedereen z’n naaste buurman op de tribune nadoet en een wave door het voetbalstadion gaat rollen.

Spectrum van waves

Om nog even in de metafoor van de wave in het stadion te blijven: de vergelijking die dit veel-deeltjessysteem beschrijft, moet onder meer kunnen voorspellen wat de golflengte van de wave op de tribune is, en hoe snel die door het stadion rolt.

Fysische veel-deeltjessystemen vertonen meestal een heel spectrum van mogelijke waves – groot, klein, snel, langzaam, linksom, rechtsom. Maar er is een belangrijke tweedeling: kent zo’n systeem een kleinst mogelijke wave, of niet? In het eerste geval heeft het systeem een spectral gap, anders niet. Als er wel een spectral gap is, kan er pas een wave ontstaan als zeg minstens twintig mensen in één vak afspreken om tegelijk de armen omhoog te doen.

De spectral gap (of band gap) is geen speeltje voor theoretici. De grootte van de band gap bepaalt bijvoorbeeld de kleur licht die een ledje uitzendt. Een led bestaat uit een piepklein stukje halfgeleider – dat wil zeggen, vele miljarden atomen – die samen lichtgolven produceren als je er een elektrische spanning overheen zet. De doorbraak van led-verlichting kwam pas, toen iemand er in slaagde een halfgeleider te maken met een zodanige band gap, dat die blauw licht uitzendt.

Voor het Standaardmodel, dat het gedrag van alle bekende elementaire deeltjes beschrijft, betekent de spectral gap dat voor die deeltjes een minimale massa geldt. Was dat niet zo, dan zou alle materie spontaan vervallen naar steeds lichtere deeltjes, totdat slechts deeltjes met massa nul overblijven. Dan hou je een leeg heelal over.

Robinson-tegels

Wat hebben deze drie wiskundigen, Toby Cubitt, David Perez-Garcia en Michael Wolf, nu precies aangetoond? Ze construeerden een quantum-veeldeeltjessysteem, waarbij de individuele deeltjes en de invloed die ze op elkaar uitoefenen corresponderen met een betegeling van het platte vlak met een speciaal setje van zes tegels, de Robinson-tegels. Hoe meer deeltjes, hoe groter het betegelde oppervlak.

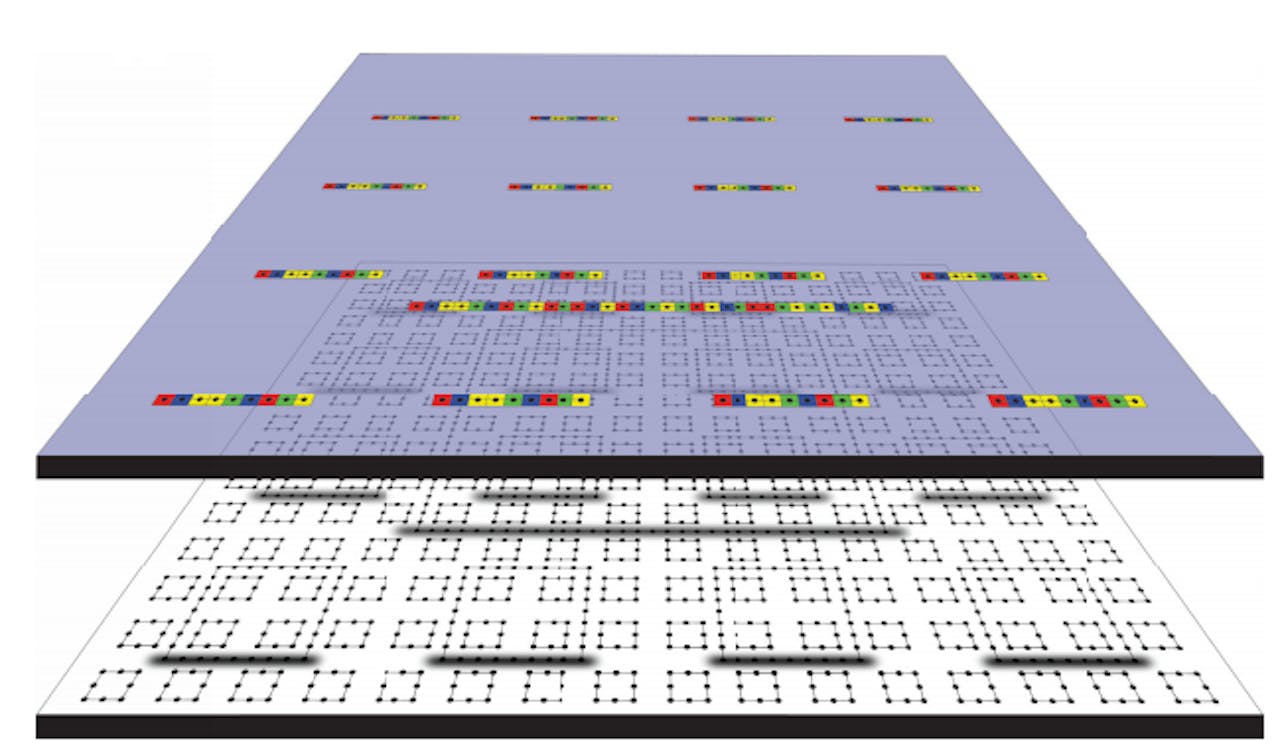
Schema hoe een rooster van quantum-deeltjes in verband wordt gebracht met een a-periodieke betegeling, en die weer met een verzameling Turingmachines die al of niet ooit stoppen met hun berekening.
Nature

Eeuwenlang werd gedacht dat als je met een setje tegels een plat vlak zonder kieren kunt betegelen, dit altijd een zich herhalend patroon oplevert, zoals elke bakstenen muur of badkamervloer laat zien. Maar een Robertson-betegeling vertoont allerlei patronen die zich, naarmate de betegeling groter wordt, bijna herhalen, maar net niet, en dit op steeds grotere schaal.

Dit levert een quantum-veeldeeltjessysteem op, dat als het ware nooit kiest tussen definitief wel of niet een spectral gap vertonen naarmate het aantal deeltjes groter wordt. De eigenschappen van normale systemen kunnen best nog flink veranderen als je van drie naar vier deeltjes gaat, maar dat verschil wordt al minder als je het aantal deeltjes uitbreidt van tien naar elf, en de verschillen worden verwaarloosbaar als je van 100 naar 101 deeltjes gaat. Voor natuurkundigen is duizend deeltjes in dit opzicht al gelijk aan oneindig.

Maar het quantum-veeldeeltjessysteem van Cubitt en collega’s blijft op een onvoorspelbare manier switchen tussen gap en gapless naarmate er deeltjes bijkomen. In de limiet naar oneindig gebeurt dit oneindig vaak, zodat de vraag ‘heeft dit systeem een spectral gap of niet?’ onbeslisbaar is.

Millenniumprobleem

Hoewel het in het artikel in Nature niet expliciet genoemd wordt, is dit probleem nauw verwant aan één van de Clay Millennium-problemen, die elk een miljoen dollar waard zijn. De excentrieke wiskundige Grigori Perelman loste er een op in 2010, maar weigerde vervolgens de miljoen dollar te incasseren.

In dit geval gaat het om de Yang-Mills gap conjecture (‘hiaatvermoeden’). Yang-Mills theorieën gaan over de wisselwerking tussen elementaire deeltjes. Neem als simpelste voorbeeld de kern van een waterstofatoom, die uit één proton bestaat (alle andere atoomkernen bestaan uit klompjes protonen en neutronen). Een proton is geen elementair deeltje, omdat het volgens het Standaardmodel bestaat uit drie quarks die in een razend tempo gluonen, ‘lijmdeeltjes’, met elkaar uitwisselen. Daarom is zelfs één proton een quantum-veeldeeltjessysteem.

In deeltjesversnellers worden nooit losse quarks aangetroffen: het zijn altijd paren of drietallen. Door het Yang-Mills vermoeden te bewijzen, zou je bewijzen dat naakte quarks niet voor kunnen komen. Met allerlei slimme benaderingsmethoden en veel computerkracht hebben natuurkundigen de laatste jaren wel zeer aannemelijk gemaakt, dat de natuurwetten inderdaad naakte quarks verbieden, maar een formeel wiskundig bewijs is niet geleverd.

Op dit punt verschilt Van Zaanen trouwens van mening met Cubitt en collega’s. Hij is er van overtuigd dat die benaderingsmethodes waterdicht zijn, zodat dit deel van het probleem wel beslisbaar is. Zaanen: “Toch is dit een eye-opener. We dachten dat die spectral gap nu juist het simpelste probleem van quantum-veeldeeltjessystemen was, en dat we dat helemaal door hadden.”

Technische toepassingen

In een begeleidend persbericht van het University College in Londen stelt Pérez-Garcia dat dit fascinerende mogelijkheden opent: “Onze resultaten laten zien, dat zelfs het toevoegen van één deeltje aan een klomp materie in principe de eigenschappen daarvan drastisch kan veranderen. Dit soort nieuwe fysica vindt later vaak technische toepassingen.”

Om het nog iets concreter te maken: het is in principe mogelijk, dat een stuk stroomdraad van 10²⁵ metaalatomen niet supergeleidend is, maar na toevoegen van nog één metaalatoom plotseling wel supergeleidend wordt. Zo’n plotselinge verandering van een collectieve eigenschap van materie heet een fase-overgang. Een fase-overgang die we allemaal kennen is die van water in ijs. Uitgaande van water van 0 graden Celsius, is een oneindig kleine daling van de temperatuur theoretisch genoeg om al het water in ijs van 0 graden Celsius te veranderen.

Maar een fase-overgang waarbij een bijna oneindig kleine toevoeging van materie de overgang van de ene naar de andere toestand veroorzaakt zou nieuw zijn in de natuurkunde. Welke mogelijkheden dat opent om nieuwe, exotische materialen te maken, die je zou kunnen toepassen in de nanotechnologie, is nog onontgonnen terrein.

Beslist onbeslisbare stellingen

De stellingen van Gödel vertonen een verre verwantschap met een klassieke paradox: ‘Alle Kretenzers zijn leugenaars, zei de Kretenzer.’ Gödel bedacht rond 1930 een methode om de regels van de wiskunde als het ware over zichzelf te laten praten, en dan iets te zeggen wat neerkomt op ‘deze stelling is niet waar’.

Dat kan een flauwiteit lijken – dat was destijds ook de eerste reactie van sommige wiskundigen – maar zelfs het feit dat één stelling bewezen onbeslisbaar is, slaat de bodem weg onder het idee dat de wiskunde een gesloten systeem is, dat je ooit ‘af’ zou kunnen krijgen, waarna alle wiskundigen met vervroegd pensioen kunnen. Sindsdien zijn trouwens ook voorbeelden van inhoudelijke stellingen ontdekt die onbeslisbaar zijn.

Alan Turing bedacht rond diezelfde tijd het principe van de universele, programmeerbare rekenmachine, ofwel de computer. Lang voor het eerste exemplaar gebouwd was, zag hij al in dat zelfs een computer met onbeperkte rekenkracht en geheugen niet elk probleem op kan lossen, met name niet het zogeheten stop-probleem.

Als je een computer een klus geeft, zal hij in sommige gevallen de klus klaren, maar in andere gevallen zal het programma in een lus terechtkomen en nooit meer stoppen. Het stop-probleem vraagt naar een algemene methode om voor elk willekeurig computerprogramma te bepalen of het ooit zal stoppen.

In een beroemd gedachtenexperiment nam Turing aan dat hij beschikte over een computerprogramma STOP dat het stop-probleem aankon. Vervolgens gaf hij STOP de opdracht het programma STOP te beoordelen. Stopt STOP dan? Turing liet op die manier zien dat een programma als STOP niet kan bestaan. Het stop-probleem is onbeslisbaar, net zoals je niet kunt beslissen of de Kretenzer wel of niet liegt.