Sommige Amsterdamse ouders pikten het niet dat hun kind niet op de favoriete school werd geplaatst. Ze eisten via een rechtszaak dat hun kind mag ruilen met andere kinderen die ook niet op de eerste voorkeur terecht kwamen. De rechter gaf deze ouders ongelijk. Aan het gehanteerde matchingsysteem mag niet achteraf gemorreld worden, omdat dit ‘strategisch’ kiezen zou belonen.
Het is bijna niet uit te leggen waarom er niet geruild mag worden: in sommige gevallen zouden twee leerlingen die van plek ruilen, allebei op een school terecht komen die ze hoger op hun vooraf ingediende voorkeurslijstjes hadden staan. Waarom mag ruilen niet, als twee leerlingen dat allebei willen en er niemand nadeel van heeft?
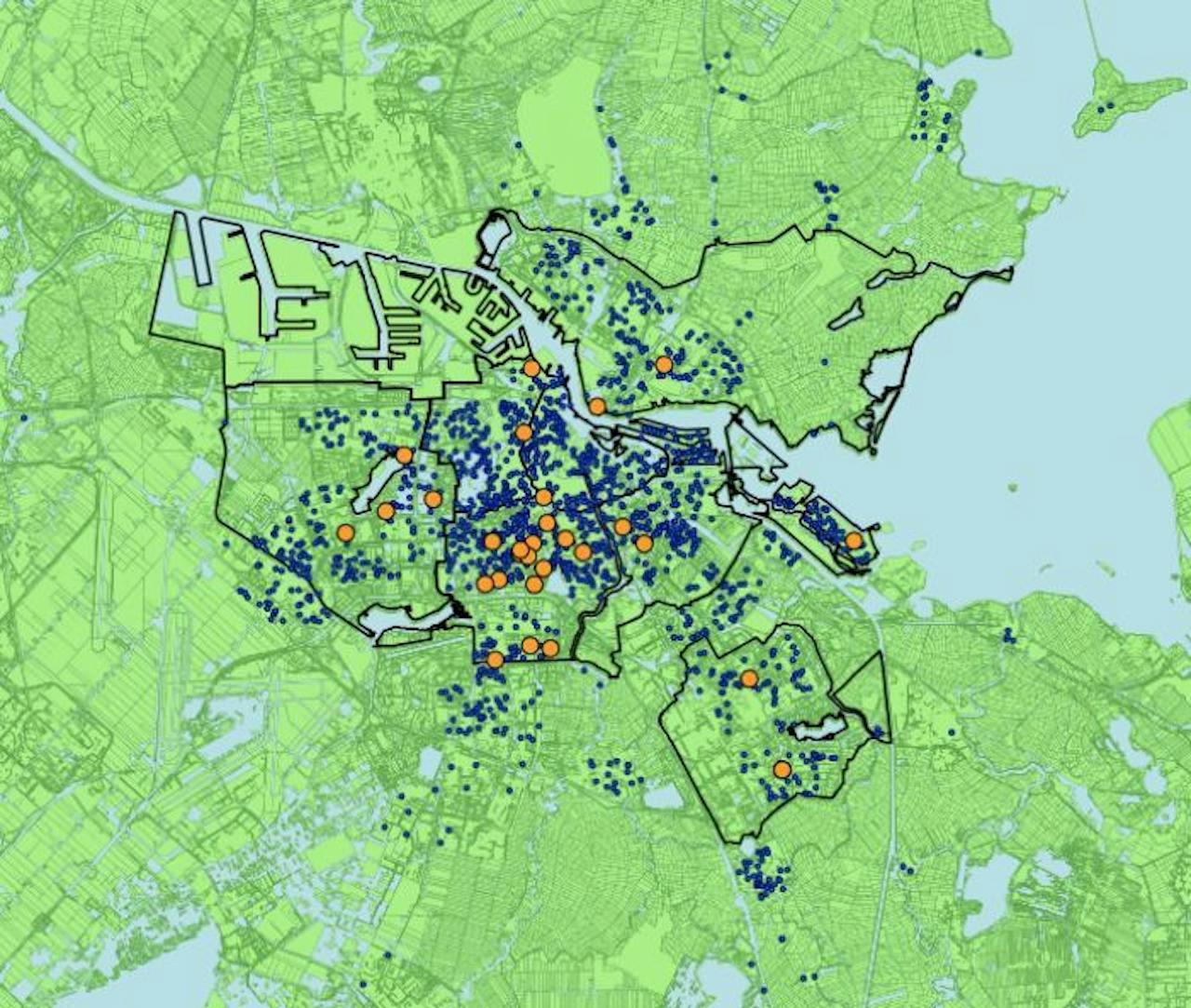
Amsterdamse middelbare scholen (oranje) trekken leerlingen uit een veel groter gebied (blauw). Vergeleken met het oude plaatsingssysteem komen dit jaar minder leerlingen terecht op de school die ze als eerste kozen, maar meer leerlingen in hun favoriete top 3 en top 5. De Osvo vindt dat dit nieuwe systeem ‘de pijn eerlijker verdeelt’ dan het oude.
P. GautierHommeles
Ieder jaar is het weer hommeles rond de keuze van een middelbare school in Amsterdam. Er zijn een paar zeer populaire scholen die doorgaans te veel aanmeldingen krijgen, zoals het Barlaeus Gymnasium en St. Ignatiusgymnasium. Het overschot wordt door de Osvo, de vereniging van Amsterdamse schoolbesturen, verdeeld over de overige scholen.
Tot 2014 mocht iedereen in de eerste plaatsingsronde maar één school uitkiezen. Als die te veel aanmeldingen had, kon je worden uitgeloot en volgde een nieuwe inschrijving voor de tweede ronde, voor scholen die nog niet vol zaten. En een derde ronde (wie dan nog geen plek had, kreeg er een toegewezen door een commissie van de Osvo).
In dat oude systeem – onder wiskundigen en economen bekend als ‘Boston’ – kon het voorkomen dat achteraf twee leerlingen tot wederzijds voordeel konden ruilen. Maar daar ontstond toen geen ophef over, omdat mensen dat niet van elkaar wisten. Dit jaar is dit dankzij internetfora wel een steen des aanstoots geworden.

Welke omgeving heeft een kin nodig om goed te kunnen functioneren?
Flickr.comSpurten op de scooter
Ambitieuze ouders wilden het uiteraard ook in het oude systeem niet op een loting laten aankomen. “Ik weet van mensen die van dag tot dag, of zelfs van uur tot uur via de websites van scholen in de gaten hielden op welke school nog plaats was. Dan spurtten ze daar in het laatste kwartier voor de sluiting van de inschrijving op een scooter naartoe om hun aanmelding nog te wijzigen”, zegt Pieter Gautier, econoom aan de Vrije Universiteit Amsterdam en adviseur van de Osvo op dit gebied.
De Osvo wilde al langer van dit jaarlijkse circus af. Er moest een systeem komen waarbij iedereen één keer een voorkeurslijsje van scholen indiende, waarna een computer de beste mogelijke plaatsing zou bepalen. Toen Alvin Roth en Lloyd Shapley in 2012 de Nobelprijs van de Economie wonnen voor dit type matching-problemen, vestigde dit de aandacht op het Gale-Shapley algoritme. Dit is een – overigens al in 1962 bedachte – methode om een groot aantal leerlingen die elk een voorkeurslijstje indienen ‘optimaal’ over scholen van hun voorkeur te verdelen. ‘Optimaal’ is in dit verband een complex begrip; je kunt allerlei criteria aanhouden voor wat optimaal is, en uiteindelijk is het een waardeoordeel wat je het belangrijkst vindt.
Ruilmateriaal
Een belangrijke eigenschap van Gale-Shapley (ofwel DA met single tie-breaking, DA-STB) is, dat de oplossing ‘ex-post Pareto efficiënt’ is. Dit wil zeggen: in de uiteindelijke matching zijn er geen twee leerlingen die met elkaar willen ruilen, want het kan niet zo zijn dat ze dan allebei op een school terecht komen die hoger op hun voorkeurslijstje staat.
De Osvo heeft echter gekozen voor een variant van dit algoritme (DA with multiple tie-breaking, DA-MTB) die niet ex-post Pareto efficiënt is. Het is niet uitgesloten dat paren leerlingen achteraf willen ruilen. In de Amsterdamse matching van dit jaar komt dit inderdaad voor. Over dit door de Osvo verboden ruilen-achteraf ging het door een groep ouders aangespannen kort geding, wat ze inmiddels verloren hebben.
Waarom vond ook de rechter dat ruilen niet mag? Gautier: “Als dat wordt toegestaan, is de procedure niet meer bestand tegen strategisch kiezen. Als mensen dat van tevoren weten, zullen sommige mensen hun echte voorkeur op 1 zetten en op 2, 3, 4 de populairste scholen, ook al willen ze daar niet echt naar toe. Want dat is goed ruilmateriaal.” De Osvo vreesde zelfs, dat in deze situatie een zwarte markt voor ruilplaatsen zou ontstaan, waarbij ouders tegen elkaar op gaan bieden voor een populaire plek.
Eerlijke voorkeuren
De Osvo hecht er grote waarde aan, dat leerlingen/ouders ‘eerlijke’ voorkeurslijstjes van scholen indienen. Die zijn idealiter gebaseerd op hoe goed de school aansluit op de wensen en behoeftes van de leerling, niet op een inschatting van hoe groot de kans is dat je op je eerste keus of in je top 3 een plek krijgt.
Bij de instructies voor de inschrijving wordt expliciet door de Osvo beloofd, dat je er nooit op achteruit kunt gaan door een eerlijke voorkeurslijst voor zoveel mogelijk (maximaal tien) scholen op te geven. Als ruilen achteraf wordt toegestaan, klopt dat niet meer. Dat ziet Osvo als het breken van een belofte en een beloning voor mensen die toch strategisch kozen.
Strategisch kiezen speelde in het oude systeem Boston een grote rol, maar ook dit garandeerde geen stabiele oplossing. Wat is er eigenlijk tegen strategisch kiezen? Waarom is het niet ‘eerlijk’ als je de kans om werkelijk op een school geplaatst te worden laat meespelen bij je voorkeur? Hier komt mogelijk een typisch Amsterdamse aap uit de mouw, namelijk de tegenstelling tussen een socialistisch getinte gemeente en de grachtengordel. Gautier: “Zowel mensen uit kansarme als uit rijke buurten doen aan strategisch stemmen. Maar die uit rijke buurten blijken daar handiger in te zijn, dus die profiteren daar meer van.”
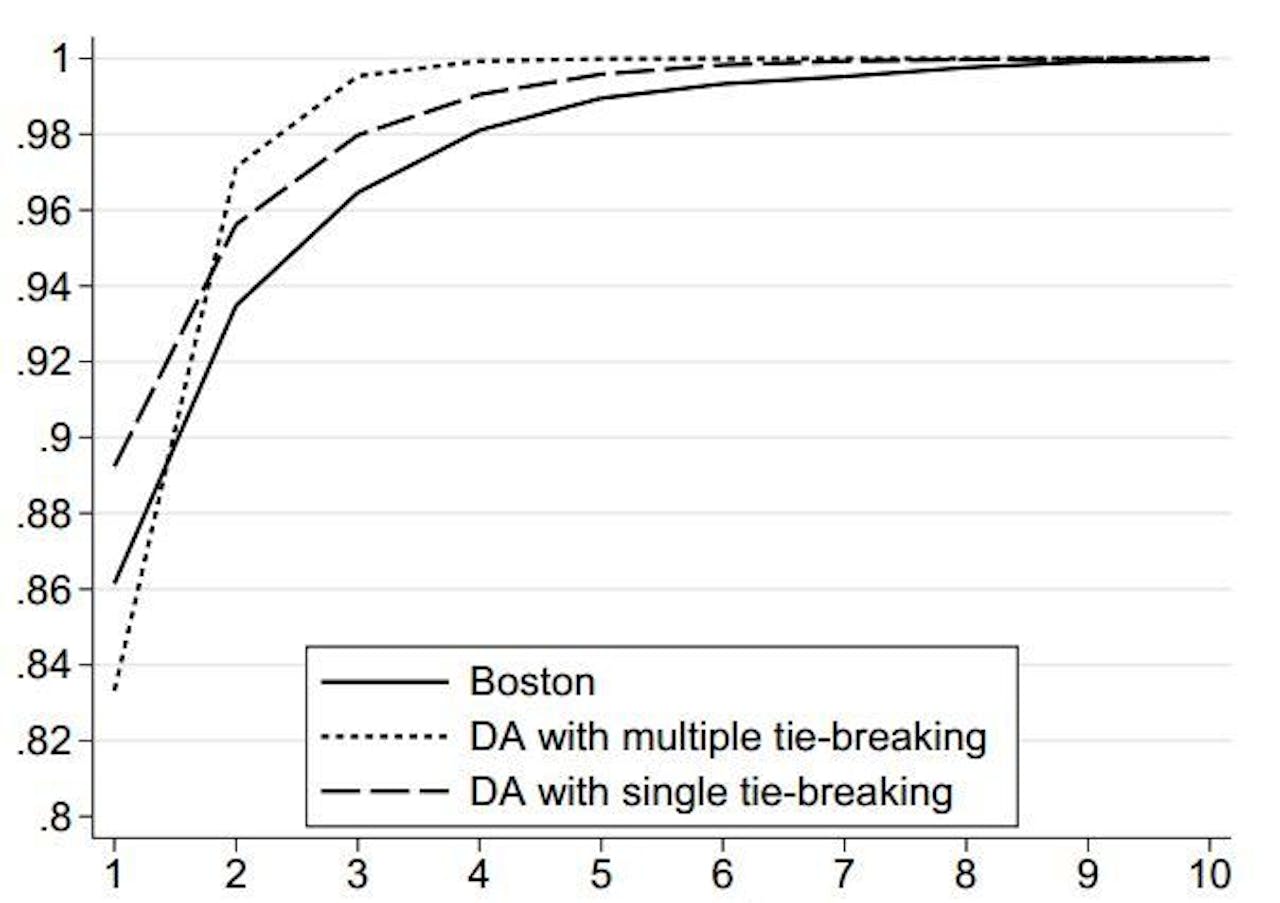
Vergelijking van drie matchingsystemen op grond van computersimulaties: het oude (Boston), het systeem nu (DA with multiple tie-breaking), en het oorspronkelijke Gale-Shapley systeem (DA with single tie-breaking). De lijnen geven aan, welk aandeel van alle scholieren geplaatst is in de top-n van het eigen voorkeurslijstje. Respectievelijk 96, 98 en 99,5 procent krijgt een plaats in de eigen top 3. De Osvo vindt dat DA multiple tie breaking ‘de pijn het eerlijkst verdeelt’: de minste scholieren vallen buiten hun top 3 of top 5.
P. GautierOnhoudbaar
De rechter heeft nu dus de Osvo gelijk gegeven. Als de klagende ouders hun zin gekregen hadden, was het hele systeem (DA multiple tiebreak) onhoudbaar en had de Osvo volgend jaar weer een nieuw systeem moeten invoeren. Overigens is dat precies wat de Amsterdamse wethouder onderwijs Simone Kukenheim (D66) al geroepen heeft. Zij wil er vanaf.
Volgens de Osvo is deze matching gemiddeld het beste voor alle leerlingen. Technocratisch bekeken is daar wat voor te zeggen (zie de grafiek die de drie systemen vergelijkt), maar de Osvo had natuurlijk moeten bedenken, dat sommige ouders en leerlingen het niet accepteren dat ze achteraf niet mogen ruilen. Zelfs niet als beide partijen daar voordeel van hebben. Die strijd moeten ze dan ieder jaar opnieuw weer gaan voeren, waarschijnlijk tot in de rechtszaal.

