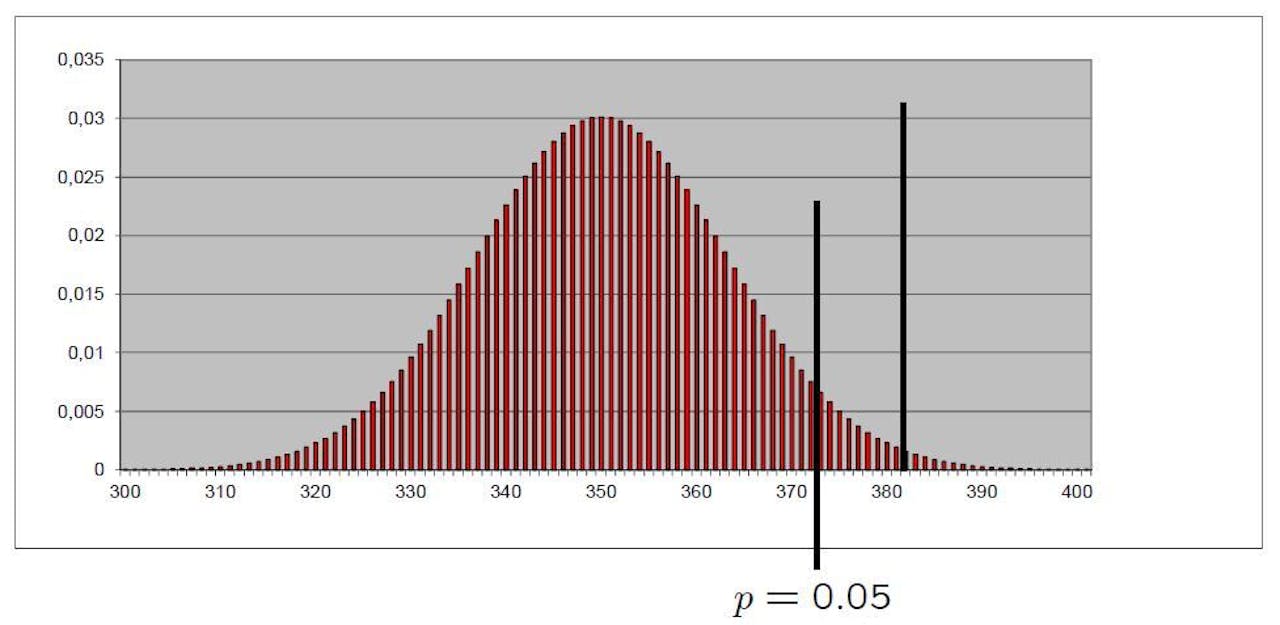
Wetenschappers roepen niet zo maar wat, die melden alleen ‘significante’ resultaten. Maar de getalsmatige grens voor wat ‘significant’ is, vormt maar al te vaak het alibi om ondermaats onderzoek te rechtvaardigen. En juist zulk onderzoek wordt gretig opgepikt door de media.

Peter Grünwald is een wiskundige met een niet geringe missie. Hij wil dat onderzoekers fundamenteel andere statistiek gaan gebruiken om hun experimenten te duiden. Zeker in de sociale wetenschappen en de medische wereld is dat bijna vechten tegen de bierkaai. De principes van wat ‘significant’ is en wat niet, rond 1935 geformuleerd door Fisher, Neyman en Pearson, zijn inmiddels verworden tot wetenschapsdogma. Er is een standaard softwarepakket voor, SPSS, zodat de medicus of psycholoog zijn experimentele gegevens in kan voeren en naar de wiskunde geen omkijken meer heeft. Moet dat allemaal op de schop?
Fetisjisme
Op de Nederlandse Wiskunde Dagen, een jaarlijkse bijeenkomst van honderden wiskundigen en wiskundeleraren, eind januari, hield Grünwald de afsluitende lezing. Hij is senior onderzoeker bij het Centrum voor Wiskunde en Informatica en hoogleraar statistiek in Leiden. Grünwald liet zijn publiek met hun Smartphones online stemmen over de vraag, of een erotisch plaatje dat ze te zien hadden gekregen, straks links of rechts op het videoscherm geprojecteerd zou worden.
Een soortgelijk experiment deed psycholoog Daryl Bem in 2011. Hij publiceerde zijn bevindingen in het belangrijkste tijdschrift van de sociale psychologie, Journal of Personality and Social Psychology. Alleen als de plaatjes erotisch waren, raadden zijn proefpersonen significant (p < 0,05) vaker dan vijftig procent goed. Dat was groot nieuws, tot in The Oprah Winfrey Show aan toe. Het riep ook veel kritiek op, onder andere van de Amsterdamse psycholoog Eric-Jan Wagenmakers, ook iemand die vindt dat de wetenschap fetisjisme bedrijft met ‘p < 0,05’.
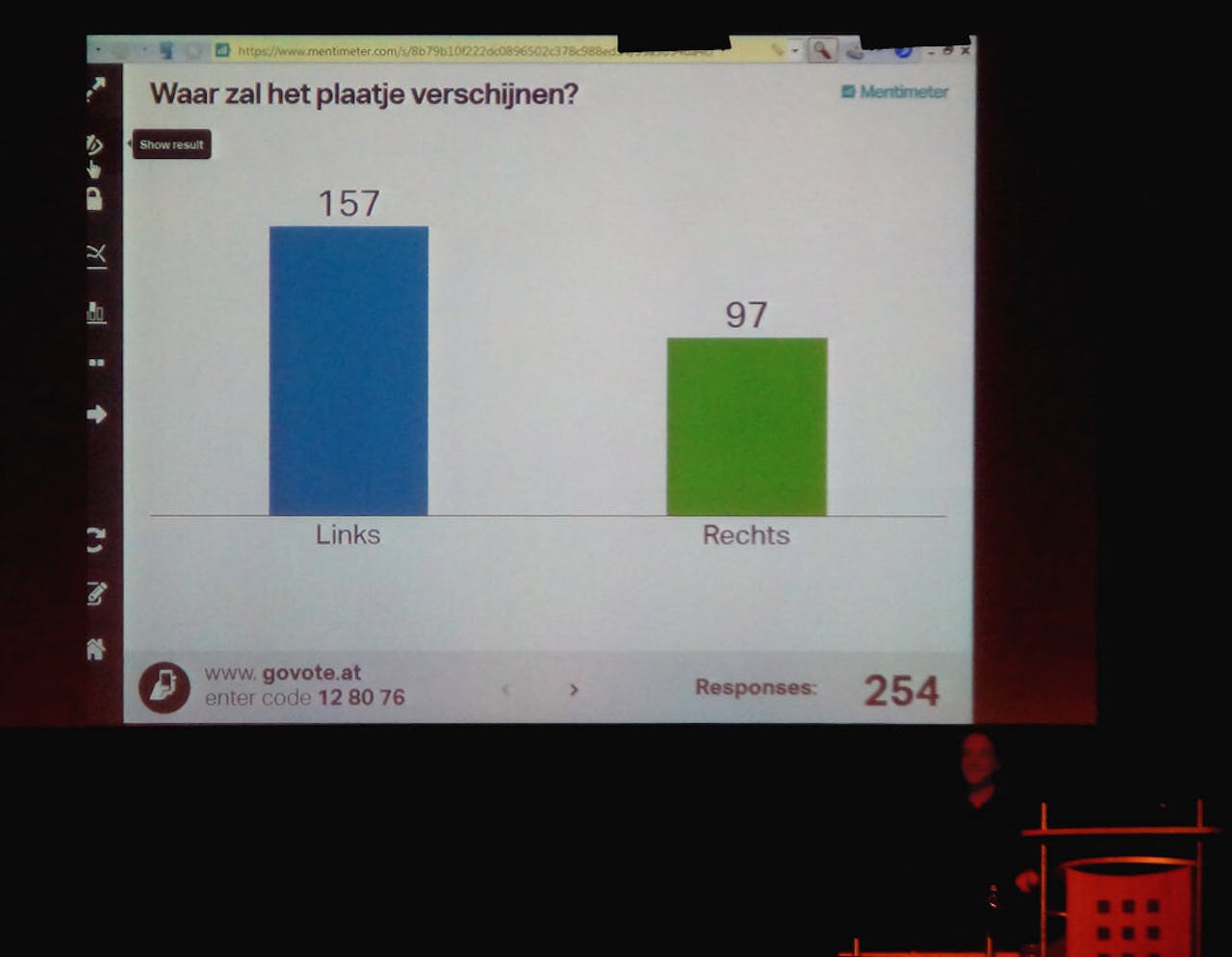
Peter Grünwald demonstreert zijn paranormale statistiek tijdens de Nederlandse Wiskunde Dagen. Het publiek kon via de eigen smartphone stemmen of een erotisch getint plaatje zometeen links of rechts op het scherm zou verschijnen. Bij blind gokken, krijgen beide kanten ongeveer evenveel stemmen. Het grote verschil tussen ‘links’ (correct, 157 stemmen) en ‘rechts’ (incorrect, 97 stemmen) levert een p-waarde veel kleiner dan 0,05 op. Is de zaal ‘dus’ significant paranormaal begaafd?
Arnout Jaspers‘Broccoli helpt tegen autisme’
De kritiek op het significantiecriterium komt van diverse kanten. Het simpelste bezwaar is, dat het zo slap is: als je welk experiment dan ook twintig keer herhaalt, vind je doorgaans één keer een significant resultaat en kan je er een wetenschappelijk artikel over publiceren. Als het een sexy onderwerp betreft, haalt het ook nog de krant en misschien zelfs de talkshows op televisie.
Hoe dat werkt, wordt prachtig geïllustreerd door een komische strip over hoe groene zuurtjes acne veroorzaken . “Als je van tevoren besluit dat je het experiment twintig keer doet, kun je daarvoor een statistische correctie toepassen. Maar als verschillende onderzoeksgroepen hier mee bezig zijn, terwijl ze dit niet van elkaar weten, hoe corrigeer je daar dan voor?”, vraagt Grünwald.
Je kan denken dat het probleem nog wel meevalt, als slechts één op de twintig berichten van het type ‘broccoli helpt tegen autisme’ ongefundeerd is – wat in academisch jargon ‘niet-reproduceerbaar’ heet. Maar het is veel erger: in een geruchtmakend arikel uit 2005 schatte hoogleraar John Ioaniddis (Stanford Universiteit) dat dertig procent van zelfs de meest geciteerde medische onderzoeksresultaten niet-reproduceerbaar zijn. Dat komt vooral door de zogeheten publication bias. Wetenschappelijke tijdschriften willen geen artikelen met de boodschap ‘broccoli doet niets met autisme’, dus worden alle mislukte pogingen om een significant verband tussen het een en het andere aan te tonen niet eens ingestuurd. Wat overblijft is daarom voor een groot deel van het type ‘groene zuurtjes veroorzaken acne’.
Bron van ellende
Een ander bezwaar van de p-waarde is, dat het een soort omkering van de bewijslast uitlokt, de prosecutor’s fallacy (de aanklagersdwaling, zie kader onderaan dit artikel). ‘Een bron van ellende’, noemde Grünwald dit in zijn lezing. Een p < 0,05 zegt: Gegeven deze nulhypothese (mensen zijn niet paranormaal begaafd), is de kans op deze data (387 van de 700 mensen stemmen correct) kleiner dan 5 procent. Bijna onvermijdelijk interpreteren mensen dit als de bewering: gegeven deze data (387 van de 700 mensen stemmen correct), is de kans dat de nulhypothese waar is, kleiner dan 5 procent. Dus zou de kans dat mensen wel paranormaal begaafd zijn, groter zijn dan 95 procent.
De meeste mensen – zelfs wiskundigen- hebben intuïtief de neiging om deze omkering te maken. Een bekend voorbeeld dat illustreert dat beide kansen in de prosecutor’s fallacy enorm kunnen verschillen gaat als volgt. Stel dat je over een willekeurig iemand vertelt dat hij professioneel basketballer is. Hoe groot schat je de kans in dat hij langer is dan 1 meter 90? Stel nu dat iemand jou zegt dat een willekeurig persoon langer is dan 1 meter 90. Hoe groot schat je dan de kans in dat hij professioneel basketballer is? Grünwald: “Hoewel het in sommige contexten makkelijk is, bijvoorbeeld bij die basketballer, is het correct redeneren over voorwaardelijke kansen – dus het vermijden van de prosecutor’s fallacy – duidelijk iets waar de menselijke geest niet voor gemaakt is.”

Enige significante resultaten van wetenschappelijk onderzoek naar het verband tussen het een en het ander.
P.GrünwaldOptional stopping
Wat je bij het rekenen met de p-waarde ook niet mag doen, is optional stopping. Stel, je doet een experiment met honderd proefpersonen om te kijken of een bepaald medicijn beter werkt dan een placebo, en er rolt een p-waarde van 0,07 uit. Vervelend, want dit is net niet significant, dus het is onpubliceerbaar. De verleiding is groot om dan nog even door te gaan: misschien zakt de p-waarde onder 0,05 als ik er nog twintig proefpersonen bij neem? Zelfs als dat lukt, is dat valsspelen; de p-waarde die je nu berekent is aan deflatie onderhevig, die geeft geen eerlijke maatstaf voor significantie meer.
Medische trials moeten tegenwoordig van te voren getailleerd beschreven worden, inclusief het aantal proefpersonen. In met name de sociale psychologie zijn de regels veel minder strak. Proefpersonen voor experimenten worden hapsnap bij elkaar gesprokkeld (vaak uit klasjes eerstejaars studenten van de onderzoeker zelf), soms over een periode van maanden en op meerdere universiteiten. In de publicatie over het onderzoek staat, als het goed is, hoeveel proefpersonen in totaal gebruikt zijn, maar of dat aantal van te voren is vastgesteld of halverwege nog is bijgesteld, is vaak onduidelijk.
Test-martingalen
Hoe moet het dan wel? Grünwald: “Het is veel handiger om een methode te hebben waarbij je net zo lang door mag gaan als je wilt.” Grünwald werkt aan zogeheten test-martingalen, waarbij dat inderdaad mag, en die een waarde voor de bewijskracht van een experiment opleveren, die niet de interpretatieproblemen van de p-waarde heeft.
De term ‘martingaal’ komt uit het casino. Het is een legendarische strategie om altijd te winnen met roulette: zet alleen in op ‘rood’ en verdubbel je inzet na iedere keer dat je verliest. Netto behaal je zo inderdaad altijd een kleine winst – maar alleen in een droomwereld waar de roulettetafel geen maximum inzet heeft en je over een oneindig groot startkapitaal beschikt.
Test-martingalen zijn een generalisatie van zowel de p-waarde als de Bayesiaanse methode (zie kader over de aanklagersdwaling hieronder). De nulhypothese en een alternatieve hypothese zijn als ‘zwart’ en ‘rood’ bij roulette, en elk experimenteel resultaat is als een draai met het roulettewiel. Je bepaalt van te voren een aantal strategieën om in te zetten op een van beide of allebei, en probeert dan zoveel mogelijk virtueel geld te winnen. Als de nulhypothese waar is, is het roulettewiel eerlijk en win je op de lange termijn niets. Als de alternatieve hypothese waar is, is er in principe een strategie om beter te scoren dan toeval – dat is overigens nooit de eerder genoemde oer-martingaal – en behaal je netto winst.
“Hoe meer geld je wint, hoe meer evidentie je hebt tegen de nulhypothese. Het is sterk gerelateerd aan wat beursfondsen doen”, aldus Grünwald. “Die proberen ook altijd een beleggingsstrategie te vinden die het beter doet dan de beursindex.” Als je de virtueel verdiende winst W noemt, dan geeft 1/W je een robuust soort p-waarde, die ook geldig is met optional stopping, dus je mag zelf bepalen hoe lang je door wilt gaan met een experiment.
De onderliggende wiskunde is ingewikkeld, dus daar moet je medici of psychologen niet mee lastig vallen. Grünwald is nog bezig om de methode te vervolmaken, maar uiteindelijk zal ook die gewoon te implementeren zijn in een softwarepakket als SPSS.
“Uiteindelijk denk ik, dat je op een verhaal uitkomt dat veel simpeler is dan de p-waarde. Geld is heel tastbaar. En totdat ik klaar ben met mijn werk: maak gebruik van Bayesiaans hypothesetoetsen.”