Kierloos tegelen met de vijfhoek

Met een regelmatige, vijfhoekige tegel kun je geen vloer betegelen zonder dat er gaten of kieren overblijven. Maar er bestaan scheve vijfhoeken waarmee dat wel mogelijk is. Tussen 1918 en 1985 werden veertien van zulke tegels gevonden, en toen bleef het heel lang stil. Nu is een vijftiende exemplaar gevonden, met hulp van de computer.

19 augustus 2015

Een van de charmes van de wiskunde is, dat zelfs op elementair niveau nog nieuwe ontdekkingen mogelijk zijn. De eerste negen kierloze vijfhoek-betegelingen werden tussen 1918 en 1975 gevonden door professionele wiskundigen. Maar een Amerikaanse huisvrouw, Marjorie Rice, vond in dat jaar de tiende vijfhoek-betegeling, nadat ze over het probleem gelezen had in het populair-wetenschappelijke tijdschrift Scientific American.

Puzzel

Vlakbetegelingen zijn voor (amateur-)wiskundigen vooral een fascinerende puzzel, al zijn er connecties met de natuurkunde. De meeste vaste stoffen komen voor in kristalvorm, wat betekent dat kleine, identieke groepjes atomen op periodieke wijze de ruimte opvullen. Meestal heeft die ruimte drie dimensies, maar in het geval van extreem dunne lagen (zoals grafeen) betegelen atomen een tweedimensionaal vlak.

Tot 1985 zijn nog vier betegelingen ontdekt, maar daarna bleef het lang stil op dit front. Tot vorige week. Toen presenteerden Casey Mann, Jennifer McLoud and David Von Derau van de Universiteit van Washington Bothell de vijftiende vijfhoek-betegeling.

Kristallen

Een opzienbarende ontdekking was in de jaren zeventig, dat je met maar twee of drie tegels een quasi-periodieke betegeling kunt afdwingen. Een periodieke betegeling met die tegels zou altijd ergens gaten open laten, maar een betegeling die zichzelf bijna, maar nooit helemaal herhaalt kan wel alle gaten dichten. Dit zijn de zogeheten Penrose-betegelingen.

Vervolgens bleken er kristallen te bestaan, die het driedimensionale equivalent van een Penrose-betegeling vormen. Het kristal is dus quasi-periodiek, iets wat natuurkundigen tot dan toe niet voor mogelijk hadden gehouden.

De nieuwe vijfhoek-betegeling. Hij bestaat uit een eindeloze herhaling van identieke groepjes van drie tegels. Elk groepje bevat drie vijfhoeken, waarbij een van de drie het spiegelbeeld van de andere twee is (je kunt een scheve tegel ‘spiegelen’ door hem ondersteboven neer te leggen, met de bovenkant op de vloer).Casey Mann

Voor de puristen is het een beetje jammer dat deze nieuwe vijfhoek-betegeling door een computer gevonden is. Mann en zijn collega’s beschreven het probleem zo, dat het speuren naar nieuwe betegelingen neerkomt op het uitproberen van een zeer groot, maar eindig aantal mogelijke tegelvormen. De computer stuitte eerst op deze mogelijkheid. De onderzoekers sluiten niet uit dat er nog meer volgen.

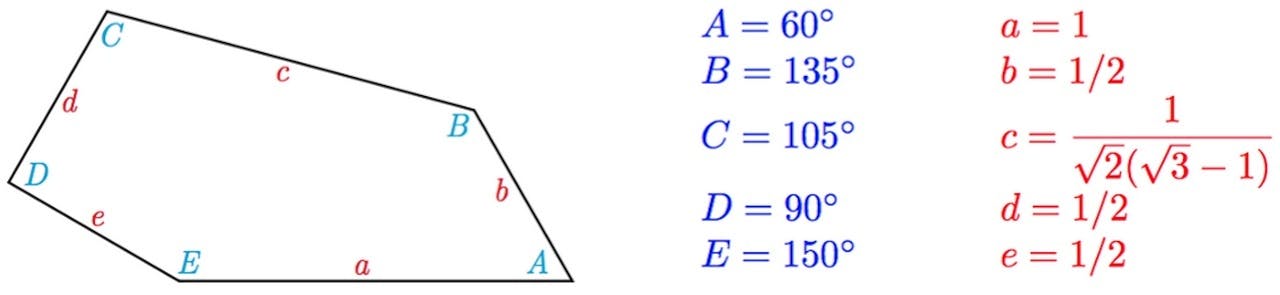
De vijftiende vijfhoek-tegel, die een exact vastgelegde vorm heeft. Zijdes a en c zijn bijna even lang; als a=1, is c = 0,9659….Bij sommige andere vijfhoek-betegelingen moet de tegel aan een aantal randvoorwaarden voldoen, maar zit er nog enige speling in de lengte van de zijden en de hoeken.
Casey Mann

Als je het tegelen van het vlak beperkt tot convexe veelhoeken, zijn vijfhoeken verreweg het interessantst. Convex betekent dat alle hoeken naar buiten uitstaan, er zitten geen deuken in de figuur. Met elke drie- en vierhoek is het mogelijk om het vlak kierloos betegelen, en het is bewezen dat er maar drie zeshoeken zijn waarmee dat lukt. Een daarvan is de regelmatige zeshoek, waarmee je het vlak betegelt in het bekende honingraat-patroon. Maar geen enkele convexe tegel met meer dan zes hoeken kan het vlak betegelen.