Naar de content

Karen Uhlenbeck wint Abelprijs voor doorbraken in abstracte meetkunde

‘Nobelprijs’ wiskunde voor het eerst toegekend aan een vrouw

Arnout Jaspers

Volgens mensen die het kunnen beoordelen, heeft Karen Uhlenbeck een paar van de belangrijkste doorbraken in de wiskunde van de afgelopen veertig jaar gerealiseerd. Ze begon als student natuurkunde, maar switchte al snel naar de zuivere wiskunde. Toch gaat haar belangrijkste werk over theorieën die het hart van de moderne deeltjesfysica vormen.

22 maart 2019

De Abelprijs is een bekroning voor een heel levenswerk, en deze wordt dus vaak aan oudere wiskundigen toegekend, zoals nu de 76-jarige Uhlenbeck. Dit is een belangrijk verschil met de wiskundeprijs die daarmee ongeveer op gelijke hoogte staat, de Fields-medaille: die wordt toegekend aan wiskundigen van maximaal veertig jaar oud, dus die zal ze nooit meer krijgen. In zekere zin maakt dat weinig uit: vrijwel alle grote wiskundigen hebben hun meest geniale prestaties al voor hun veertigste geleverd. Een winnaar van de Fields-medaille maakt daarom een goede kans om later ook de Abelprijs te krijgen, maar die bestaat pas sinds 2003.

Oeroude tweedeling

Het Abelcomité roemt Uhlenbeck als de grondlegger van de moderne geometrische analyse. Dit vakgebied overbrugt een oeroude tweedeling in de wiskunde, namelijk die tussen de visueel geöriënteerde meetkunde en de analytische wiskunde, die meer gebaseerd is op het oplossen van wiskundige vergelijkingen.

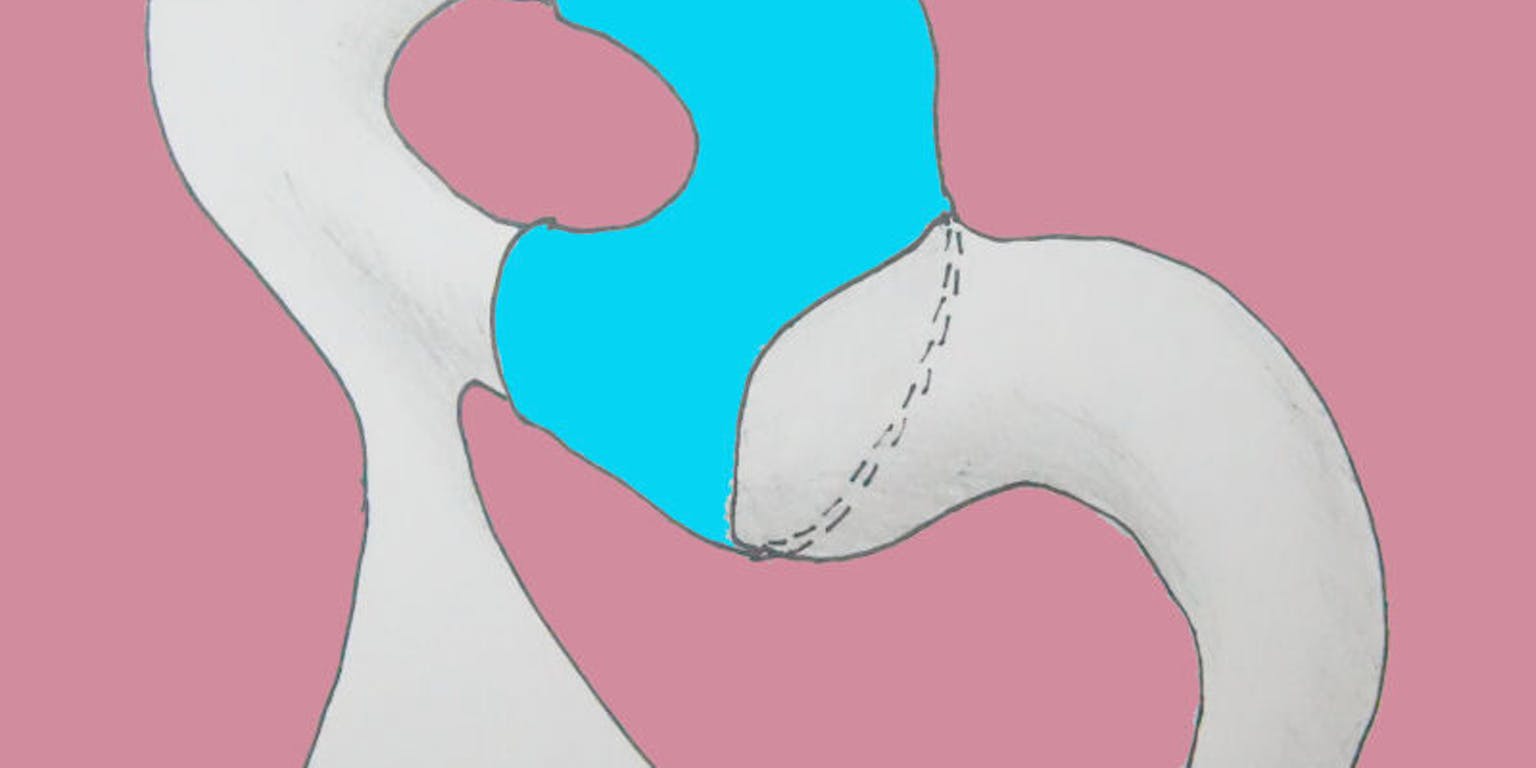
In welke positie is het elastiekje op dit voorwerp het minst uitgerekt? Dit is een strikvraag, want het elastiekje kan, zonder los te komen van het oppervlak, naar één punt inkrimpen, en dat kan in elk punt op het oppervlak.

Arnout Jaspers

Zelfs op de middelbare school leer je al vergelijkingen op te stellen voor meetkundige figuren en daar aan te rekenen, maar de moderne geometrische analyse doet dat op een veel hoger abstractieniveau, en vaak in meer dan twee of drie dimensies.

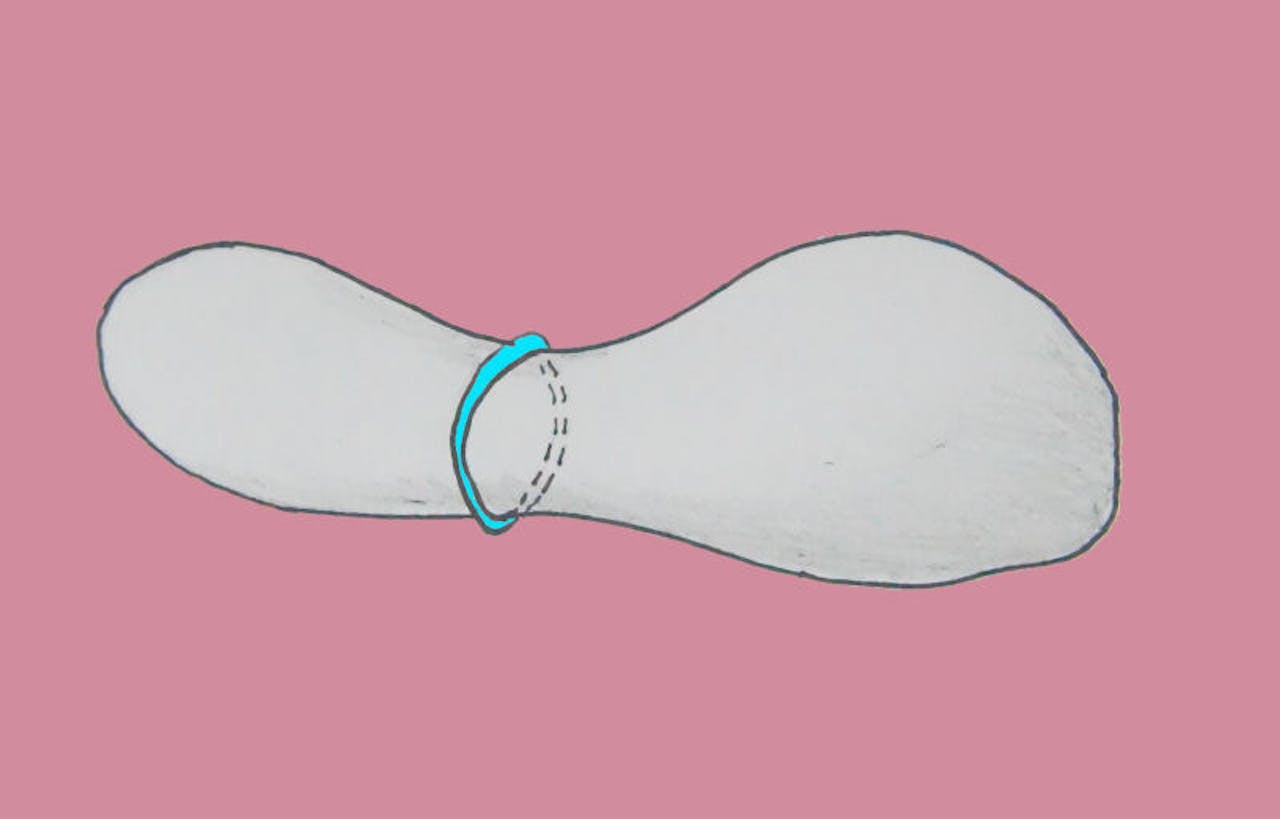
Het type vraagstukken waar Uhlenbeck zich in de jaren zeventig en tachtig op focuste, laat zich in drie dimensies illustreren door een elastiekje dat je om een voorwerp heen doet. Je kunt je voor allerlei klassen van voorwerpen afvragen op welke plek het elastiekje de minste rek voelt. In de eerste afbeelding hierboven zie je eigenlijk een nep-voorbeeld: het elastiekje kan namelijk – zonder ooit ergens van het oppervlak los te raken – inkrimpen tot één punt (wiskundigen gaan natuurlijk uit van een oneindig rekbaar, oneindig dun elastiekje dat zonder wrijving kan verschuiven over het oppervlak).

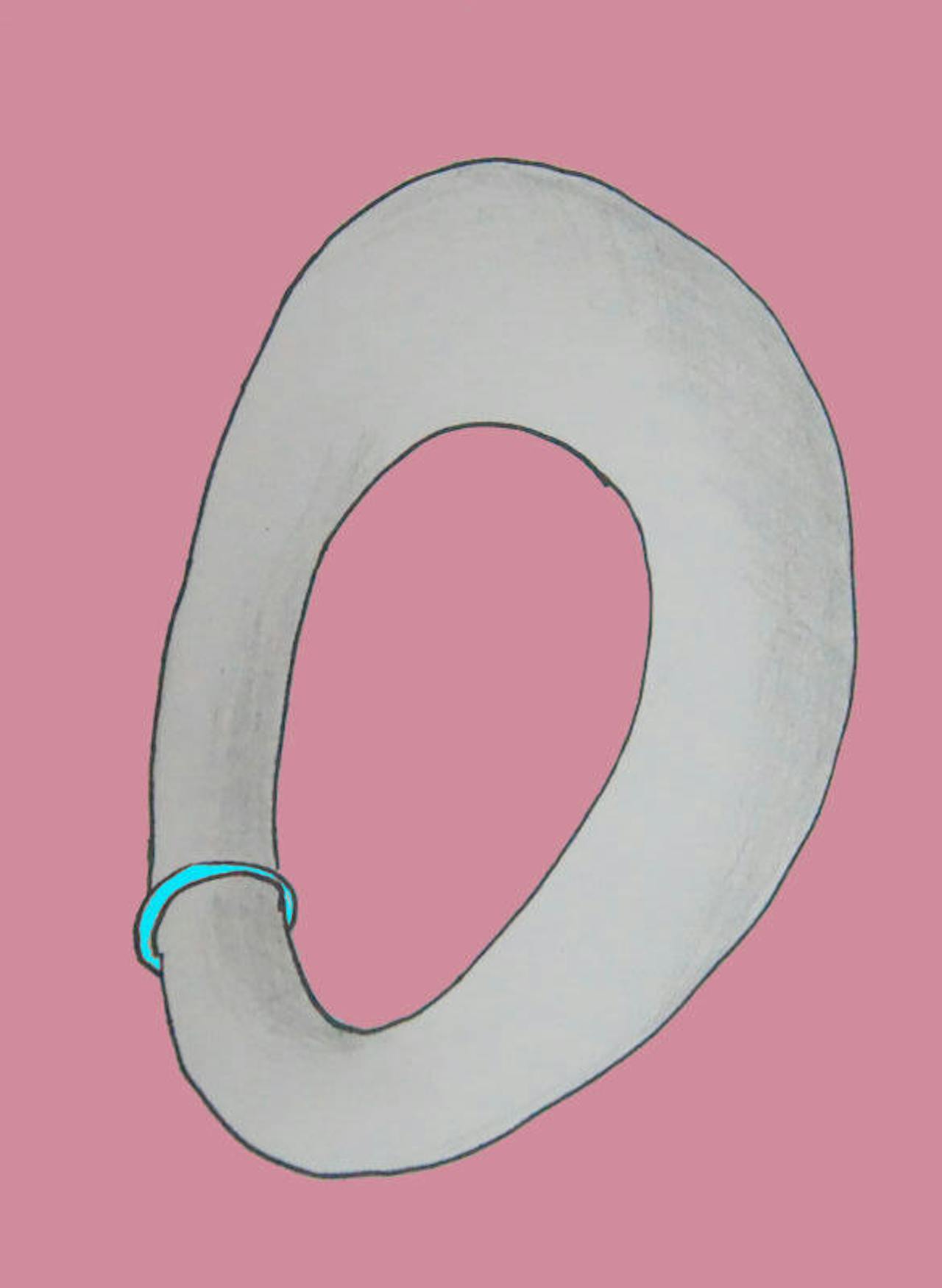
Als het elastiekje om een torus zit, kan het niet tot één punt inkrimpen; de uitrekking heeft een echt minimum.

Arnout Jaspers

Het tweede voorbeeld, hiernaast, is iets interessanter: het elastiekje kan niet onbeperkt inkrimpen, en zal ergens rond het smalste stuk van de ring (wiskundige term: torus) de minste rek voelen, en daar dus een stabiele positie innemen. Als je begint met het elastiekje rond een willekeurig deel van de ring, zal het daar spontaan naartoe glijden. Al vóór Uhlenbeck was uit de vergelijkingen die de vorm van de torus beschrijven, goed te berekenen welke positie het elastiekje zal gaan innemen.

Maar als een brede elastieken band door een ingewikkelde drie-dimensionale vorm met allerlei gaten en bulten gevlochten zit, is dit verre van simpel. Laat staan als die vorm nog een paar dimensies meer heeft, zes of zeven, zodat je er geen plaatje meer van kunt maken.

Bubbling

Uhlenbeck gebruikte geavanceerde analytische methodes om ook in deze gevallen uit te rekenen wat er met het elastiek gebeurt: vindt het spontaan de positie met de minimale rek, blijft het onderweg naar dat minimum ergens steken (in een zogeheten lokaal minimum), of verdwijnt het zelfs in één punt, zoals in de bovenste afbeelding?

Een compleet nieuwe techniek die Uhlenbeck daarbij ontwikkelde, bubbling, (gedetailleerd beschreven in dit artikel in Quanta Magazine) gaf haar de mogelijkheid om veel algemenere resultaten te boeken dan al haar voorgangers. Ontoelaatbaar versimpeld, houdt bubbling in, dat bij het verschuiven van het elastiek naar de minimumpositie, dit vaak op een eindig aantal geïsoleerde punten blijft hangen. Op die punten kun je een bel in het elastiek blazen, en omdat het oneindig rekbaar is, zit er in de uiterste limiet nog maar nul hoeveelheid elastiek in de bubble, en is die in zekere zin verdwenen en het hangpunt onschadelijk gemaakt.

Dit type vraagstukken heeft een rechtstreekse connectie met de moderne deeltjesfysica. Natuurkundige systemen ‘streven’ altijd naar de toestand met de laagste interne energie. En in de snaartheorie, de beoogde ‘theorie van alles’ speelt de natuurkunde op microscopisch kleine schaal zich af in een ruimte van tien of elf dimensies. In een reactie voor De Wereld Draait Door vertelde snaarfysicus Robbert Dijkgraaf dat hij Uhlenbecks resultaten dagelijks gebruikt in zijn theoretisch onderzoek.

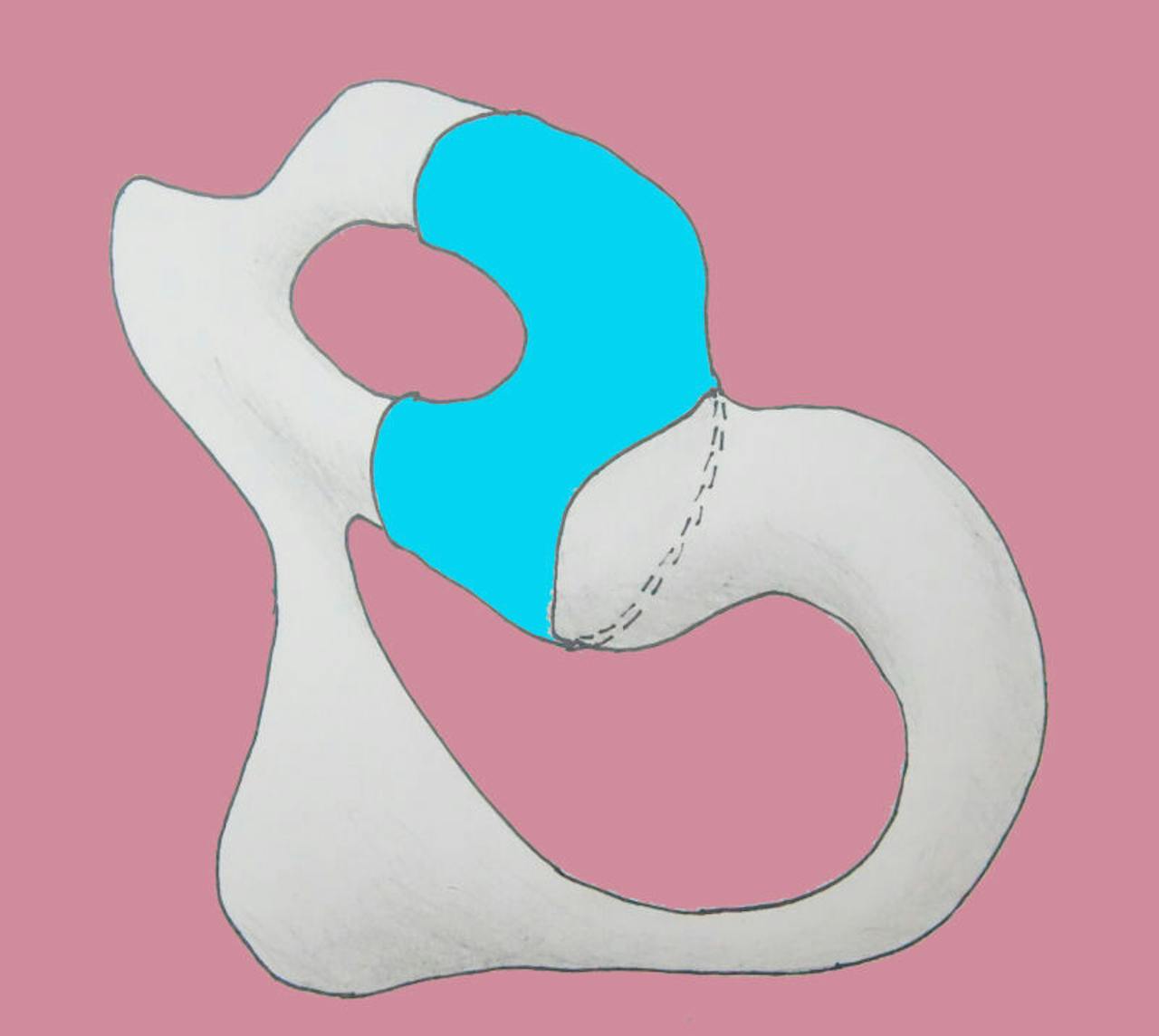
Als een elastische ‘steunkous’ in een ingewikkeld voorwerp met meerdere gaten gevlochten zit, is heel moeilijk te bepalen waar de positie met minimale rek zit, en of die positie bereikbaar is zonder de steunkous open te knippen.

Arnout Jaspers

Women and Mathematics

Hoewel ze na de bekendmaking van de Abelprijs in de media gevierd werd als een activist voor vrouwenrechten en meer vrouwen in de bèta-wetenschap, is ze pas laat in haar carrière op dat gebied actief geworden. In interviews en een autobiografische tekst op haar universitaire webpagina schetst ze een beeld van zichzelf als een typische wiskundige: iemand die voor dit vak kiest omdat je dat grotendeels in je eentje en in afzondering kunt doen.

Ze schrijft: “Ik heb altijd geweten dat ik een heel goede wiskundige was. Ik heb van nature een neiging naar abstractie en ik ben gek op ideeën op allerlei gebied. Ik hecht grote waarde aan tijd voor mezelf, om na te denken over wiskunde of andere zaken, dat maakt niet uit. Al die herrie uit de buitenwereld kan ik moeilijk mee om gaan. Ik heb er altijd moeite mee gehad om externe prikkels te verwerken.”

Als jonge wiskundige aan de universiteit werkte ze met maar weinig collega’s samen, en ze hield niet van college geven. Pas later kreeg ze in haar werk meer behoefte aan sociaal contact, en begon ze ook promovendi te begeleiden. Haar belangrijkste wiskundige werk deed ze in de jaren zeventig en tachtig; pas in de jaren negentig werd ze mede-oprichter van het Women and Mathematics_-programma aan de instelling waaraan ze toen verbonden was, het _Institute for Advanced Study in Princeton (waar Robbert Dijkgraaf nu directeur van is).

Elektronspin

Ze heeft ook een minder vergezochte connectie met Nederland: ze trouwde met de zoon van de beroemde Nederlandse natuurkundige George Uhlenbeck, die voor de Tweede Wereldoorlog met zijn vrouw naar de Verenigde Staten gevlucht was. Samen met Samuel Goudsmit had George Uhlenbeck in 1925 in Leiden ontdekt dat elektronen spin hebben: ze draaien om hun eigen as, net als de aarde, maar dan razendsnel en op een manier die zich alleen met de quantumtheorie laat beschrijven. Elektronspin en de consequenties daarvan behoren momenteel tot de basiskennis van elke natuur- en scheikundige.

Karen kwam destijds veel bij haar schoonouders over de vloer en roemt vader Uhlenbeck als een informele mentor en inspirerende persoonlijkheid. Vanwege de achtergrond van hem en zijn vrouw – jeugd in Nederlands-Indië, door de dreiging van de nazi’s verjaagd uit een welvarend, cultureel milieu in Europa – ging er voor haar als Amerikaanse een heel nieuwe wereld open.

Deeltjesfysica

Hoewel ze haar eerste studiekeus, natuurkunde, al snel afdankte om alleen nog wiskunde te doen, is haar werk vaak door de natuurkunde geïnspireerd. Dat geldt zeker ook voor haar werk aan zogeheten ijktheorieën.

IJktheorieën vormen het theoretische fundament van de huidige deeltjesfysica – kortweg aangeduid als het Standaardmodel. De Nederlanders Gerard ‘t Hooft en Martin Veltman kregen in de jaren negentig de Nobelprijs voor natuurkunde omdat ze hadden aangetoond dat ijktheorieën een bepaalde wiskundige eigenschap hebben, namelijk dat ze ‘renormaliseerbaar’ zijn. Renormaliseren is een ietwat dubieuze wiskundige truc om theorieën over elementaire deeltjes, die voor allerlei meetbare eigenschappen als de massa en de elektrische lading van deeltjes uitkomst ‘oneindig’ geven, toch een eindig antwoord op te laten leveren. Dit was typisch door natuurkundigen verzonnen wiskunde: leuk in elkaar geknutseld, en het leverde goede resultaten op, maar het moest nog door echte wiskundigen beter onderbouwd worden, en daar heeft Uhlenbeck veel aan bijgedragen.

In een interview met tijdschrift Celebratio Mathematico benadrukt ze hoe natuurkundigen ook de wiskunde verder helpen: “Ik vind dat indrukwekkend. Ik heb de indruk dat wiskundigen in sommige opzichten geen heel inventieve denkers zijn. Ze hebben een idee, en dan is het net of ze het dood slaan om er mee verder te komen. Voor de meeste mensen die aan een probleem werken gaat het idee erachter vaak verloren.” Volgens Uhlenbeck hebben natuurkundigen, ook als ze met een wiskundig probleem bezig zijn, een andere benadering: “Ze denken echt anders, maar ik ben er nooit achter gekomen op welke manier ze anders over problemen nadenken.”

ReactiesReageer