Naar de content

'Je bent er niet minder om, als je die prijs niet wint'

Interview met Fieldsmedaille-winnaar Alessio Figalli

Arnout Jaspers

Op een groot congres in Leiden praatten wiskundigen uit de hele wereld elkaar bij over differentiaalvergelijkingen: het basisgereedschap voor toegepaste wiskunde, maar ook bestudeerd om hun abstracte schoonheid.

Alessio Figalli was in Leiden als deelnemer aan Equadiff. Deze tweejaarlijkse conferentie, dit jaar georganiseerd door het Mathematisch Instituut van de Universiteit Leiden, is voor het eerst in Nederland gehouden. Meer dan vijfhonderd wiskundigen kwamen daar samen om de nieuwste ontwikkelingen op het gebied van differentiaalvergelijkingen met elkaar te bespreken. De Nederlandse wiskunde is traditioneel sterk vertegenwoordigd in deze tak van wiskunde.

Equadiff, Universiteit Leiden

De symboliek ligt voor het oprapen: de plenaire lezingen van het congres Equadiff vinden plaats in de Hooglandse Kerk, een imposant godshuis waarvan de historie teruggaat tot in de middeleeuwen. En juist als Alessio Figalli zijn slide met een belangrijk nieuw resultaat presenteert, klinkt buiten een zware donderslag.

Het wiskundig onderzoek van Figalli is zeer abstract. Zelfs een flink deel van de wiskundigen die deze dag aanwezig waren in de Hooglandse Kerk zullen zijn lezing niet tot in alle finesses begrepen hebben. De moderne wiskunde is uitgegroeid tot vele, wijd uiteenlopende specialismen.

‘Nobelprijs voor de wiskunde’

Figalli heeft doorbraken bereikt in het onderzoek naar sommige types differentiaalvergelijkingen (zie voor uitleg het kader onderaan), en kreeg daarvoor vorig jaar de Fieldsmedaille. Deze wordt elke vier jaar uitgereikt aan twee tot vier wiskundigen. De prijs wordt ook wel de Nobelprijs voor de wiskunde genoemd, maar dat is volgens Figalli heel wat anders: “Wij zijn gelukkig te jong om te denken: dat was het dan.” Immers, je moet jonger dan veertig zijn om de Fieldsmedaille te winnen, terwijl de Nobelprijs meestal aan 70-plussers wordt toegekend.

Figalli is pas 35, en ziet er minstens zo jong uit. Na een periode in de Verenigde Staten is hij nu hoogleraar aan de gerenommeerde ETH Zürich in Zwitserland. Hij kreeg de prijs voor zijn werk aan ‘optimaal transport’. In veel natuurlijke processen blijkt een optimaliseringsprincipe te gelden. Zo ‘kiezen’ lichtstralen altijd de snelste (niet de kortste) weg door een stelsel van lenzen, en neemt het oppervlak van zeepbellen altijd de vorm aan waarin de oppervlaktespanning minimaal is.

Alessio Figalli tijdens zijn lezing in de Hooglandse Kerk in Leiden.

 Arnout Jaspers

Figalli kon bewijzen dat ook de schijnbaar chaotische vorming van wolken door een optimaal transport-principe geregeerd wordt. Hoewel hij wiskundige vergelijkingen bestudeert als doel op zich, kan dit ooit toch bijdragen aan bijvoorbeeld betere weersvoorspellingen of klimaatmodellen.

Geen wonderkind

Anders dan veel gelauwerde wiskundigen, was Alessio Figalli geen wonderkind: “Ik raakte pas geïnteresseerd in wiskunde op m’n zestiende, toen ik mee ging doen aan de Wiskunde Olympiade.” Deze competitie voor scholieren wordt ook in Nederland gehouden, en resulteert na diverse voorrondes in een nationaal team dat meedoet aan de Internationale Wiskunde Olympiade. De beste deelnemers worden later vaak wereldberoemde wiskundigen.

Maar zo ging het niet met Figalli: “De meeste andere scholieren die daar aan meededen hadden al veel langer getraind dan ik, dus ik haalde het nationale team niet. Het is een sprookje dat je er alleen op talent heel goed in kunt zijn. Er is ook een heleboel training voor nodig. Toen ik de middelbare school af had, twijfelde ik nog tussen de studies natuurkunde en wiskunde, of ingenieur worden. In mijn eerste jaar wiskunde vond ik algebra interessanter. Maar in het tweede jaar en daarna voelde ik dat ik een betere intuïtie had voor differentiaalvergelijkingen. En ik vond ze simpelweg aantrekkelijk. Er zijn veel verschillende differentiaalvergelijkingen, maar veel ervan zijn mooi. En uiteraard, hoe langer je werkt aan een vergelijking, hoe meer je die gaat waarderen.”

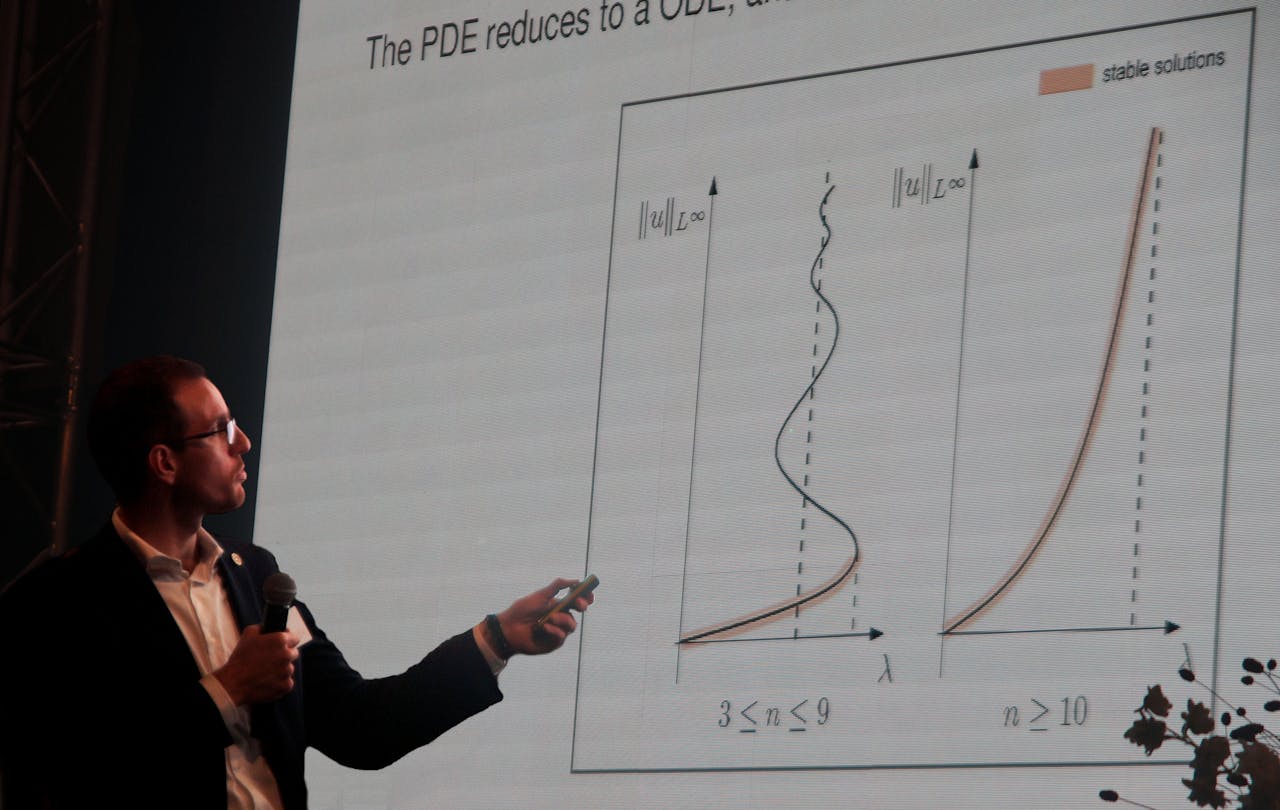
Figalli demonstreert nieuw gevonden oplossingen van semi-lineaire elliptische partiële differentiaalvergelijkingen (n is de dimensie van de ruimte waarin de vergelijking opereert).

 Arnout Jaspers

Van sommige differentiaalvergelijkingen is ook na eeuwen onderzoek nog lang niet alles bekend. Van een gewone, algebraïsche vergelijking, bijvoorbeeld x2 – 8x + 15 = 0 vind je op zeker moment de oplossing (x=3 of x=5), en dan ben je er als wiskundige wel op uitgekeken. Maar van een interessante differentiaalvergelijking vind je nooit ‘de’ oplossing. Zo’n vergelijking kun je namelijk bestuderen in ruimtes van allerlei dimensies, en onder allerlei randvoorwaarden, zodat het aantal variaties bijna onbeperkt is.
Ook is een oplossing niet één of meerdere getallen, maar een complete structuur in een meerdimensionale ruimte. Zo’n oplossing kan bijvoorbeeld het stromingspatroon van lucht rond een vliegtuig voorstellen. Maar zodra je ook maar iets aan de vorm of de snelheid van dat vliegtuig verandert (de randvoorwaarden), verandert ook de oplossing.

Publiceren als verlies

Toen Andrew Wiles na zeven jaar alleen en in het geheim werken de laatste stelling van Fermat bewees, een probleem waar wiskundigen eeuwen hun tanden op stuk gebeten hadden, vertelde hij achteraf dat het publiceren van zijn bewijs bijna voelde als een verlies: zijn unieke, intieme relatie met De Stelling zou nooit meer dezelfde zijn.

Figalli’s band met zijn vergelijkingen gaat toch wat minder diep. Op de vraag of ze voor hem eerder vriend of vijand zijn, moet hij even nadenken: “Voor mij zijn ze vooral gereedschap. Als ik begin te werken aan een probleem, en het is compleet nieuw voor me, ga ik eerst wat artikelen over het onderwerp lezen, alleen maar om te zien wat er al aan gedaan is, maar ik bestudeer ze niet heel grondig. Dan heb ik al wat intuïtieve ideeën, dat worden later educated guesses, en vervolgens gebruik je de vergelijkingen als gereedschap om resultaten te krijgen. Zo heb ik aan veel vergelijkingen gewerkt, maar die van Monge-Ampère is voor mij toch wel speciaal.” Figalli loste een al twintig jaar oud probleem omtrent de Monge-Ampère-vergelijking op, een van de vergelijkingen die ‘optimaal transport’ beschrijven.

Differentiaalvergelijkingen

De wiskundige vergelijkingen die bijna iedereen zich nog van de middelbare school herinnert, hebben als oplossing één (of meerdere) waarde(s) voor de onbekende, x. Bijvoorbeeld: f(x) = 3x + 4 = 10 heeft als oplossing x=2. De formule f(x) zegt: ‘neem een x, maak die drie keer zo groot en tel er vier bij op. Voor welk getal x levert dat 10 op?

Een differentiaalvergelijking gaat een abstractieniveau hoger. Die zegt bijvoorbeeld: ‘neem een – vooralsnog onbekende – formule voor x, noem die f(x). Neem de afgeleide van f(x), dat is f’(x). Welke f voldoet aan de vergelijking: f(x) – (f’(x))2/4 = 3 ? De oplossing is dus niet iets als x = 2 of x = 1000, maar een complete formule voor x, namelijk f(x) = x2 + 3. Je kunt zelf checken dat de vergelijking dan klopt, mits je nog weet dat de afgeleide van x2+3 gelijk is aan 2x, dus f’(x)=2x.

De differentiaalrekening is in de zeventiende eeuw uitgevonden door Isaac Newton (en gelijktijdig door Wilhelm Leibniz) om de bewegingen van planeten om de zon te berekenen. Je zoekt dan niet naar de positie van een planeet op een bepaald tijdstip, maar naar een formule die de posities van deze planeet op elk willekeurig tijdstip beschrijft.

zijn sindsdien een van de belangrijkste wiskundige gereedschappen in de bèta-vakken geworden. Zo berekenen de computermodellen die het weer en het klimaat voorspellen, in wezen zeer gecompliceerde oplossingen van de Navier-Stokes-differentiaalvergelijkingen die de stroming van gassen en vloeistoffen bepalen.

Hoewel het cliché wil dat wiskundigen eenlingen zijn, geven de meesten er juist de voorkeur aan om veel met anderen samen te werken, en Figalli is daarop geen uitzondering: “Ik praat graag met collega’s over problemen waar ik aan werk, samen voor een schoolbord. Dat is veel leuker. Ik werk ook wel samen via Skype, maar dat is toch niet hetzelfde. Er zijn momenten dat je elkaar niets te zeggen hebt, dan ben je alleen maar aan het denken. Je kan niet twee uur lang Skypen en dan tien minuten lang niets zeggen. Misschien met goede vrienden, maar niet met collega’s.”

Eureka!

Is vooruitgang boeken in een wiskundig probleem voor hem vooral gestadig zwoegen, zoals je een tunnel in een berg boort, of bestaat vooruitgang uit plotselinge doorbraken, uit eurekamomenten? Figalli: “Ik heb echt niet bij elk belangrijk resultaat een eurekamoment gehad. Soms kan dat zo lijken, maar in feite is je brein er maanden- of jarenlang op de achtergrond mee aan het werk geweest. En soms denk je dat je vooruitgang boekt, terwijl je eigenlijk probeert om met blote handen door massieve rots heen te graven. Dat is het punt waarop je moet besluiten om die tunnel te verlaten, helemaal terug naar het begin en ergens anders opnieuw beginnen. Het is emotioneel heel moeilijk om dat te doen. Maar soms spring je dan ineens naar de top.”

Het is zeker voor een wiskundige makkelijk om geobsedeerd te raken door een probleem. Figalli houdt dat liever binnen de perken: “Ik probeer mezelf te dwingen om ‘s avonds niet meer aan wiskunde te denken. Voor mij werkt het niet, de hele nacht opblijven om een probleem op te lossen. Ik heb normale slaap nodig om ‘s ochtends weer met frisse energie te beginnen.”

Is het winnen van zo’n prestigieuze prijs puur loon naar talent en werken, of komt er ook geluk bij kijken? Figalli: “Je moet al geluk hebben om het niveau te bereiken waarop je zelfs maar kan hopen om een prijs als de Fieldsmedaille te winnen. Ik heb het geluk gehad om heel goede begeleiders te ontmoeten. Daarna moet je ook nog het geluk hebben dat je wordt uitgekozen voor zo’n prijs. Er is zo’n verscheidenheid aan zaken die wiskundigen doen, het is eigenlijk appels met peren vergelijken. Het winnen van de Fieldsmedaille betekent zeker veel voor me, maar als je die prijs niet wint, ben je er echt niet minder om.”

“En voor mij is het een mixed blessing. Als ik aan het werk ben, werk ik beter, want ik ben vrijer. Ik voel niet langer die druk dat ik mensen misschien teleurstel. Anderzijds is het een extra verantwoordelijkheid. Het is moeilijker geworden om me mentaal te focussen op wiskunde. Ik moest leren om interviews en lezingen te geven voor publiek en voor schoolkinderen. Ik ben altijd uitgeput na zoiets.” Dat lijkt het juiste moment om het interview af te sluiten.

ReactiesReageer