Facebook, het internet en epidemieën gedragen zich als random netwerken.

Het internet, Facebook, of een epidemie: het zijn voorbeelden van netwerken die zo groot en veranderlijk zijn, dat we ze nooit exact in kaart zullen kunnen brengen. Maar als iets te groot is om tot in detail te kennen, kun je die details altijd nog met een dobbelsteen invullen. Zulke willekeurige netwerken leveren toch bruikbare inzichten op over de echte wereld.

3 december 2014

Onze moderne maatschappij draait op netwerken voor vervoer, energie en data die steeds complexer worden. Het is een enorme klus om ervoor te zorgen dat iedereen mobiel kan blijven bellen en naar hartenlust internetten. Eigenlijk weten we nog onvoldoende hoe we zulke complexe netwerken het beste kunnen aansturen en bestand kunnen maken tegen onverwachte storingen.

Onvolledige informatie

Het managen van netwerken wordt een stuk moeilijker als nergens volledige informatie over de toestand van het netwerk beschikbaar is. Niemand weet hoe druk het nu is op elk knooppunt van het internet. Langs welke route moet ik dan mijn data versturen om ze zo snel mogelijk aan te laten komen? Je kunt het vergelijken met het in goede banen leiden van een groot publieksevenement: als je wilt dat de mensenmassa optimaal doorstroomt terwijl niemand in het gedrang komt, volgens welke vuistregel moet ik, deelnemer en individu dat geen overzicht heeft over het geheel, mij dan gedragen?

Volgens Michel Mandjes, wiskundige aan de Universiteit van Amsterdam (UvA) en het Centrum Wiskunde & Informatica (CWI), is dit de hamvraag bij de analyse van complexe netwerken: “Zijn er regels te vinden die lokaal gelden, maar die ervoor zorgen dat het hele netwerk optimaal functioneert?” In het geval van de mensenmassa luidt regel 1: Niet duwen, maar dat is slechts een kwestie van gezond verstand.

Om dieper inzicht te krijgen in zulke complexe netwerken, vormde Mandjes met wiskundigen van diverse Nederlandse universiteiten onder de naam NETWORKS een samenwerkingsverband, dat vorig jaar 23 miljoen euro onderzoeksgeld kreeg voor de komende jaren. Op een symposium bij de KNAW, de Koninklijke Academie van Wetenschappen, kwamen op 28 november diverse onderzoekers vertellen waar ze mee bezig zijn.

Facebook-relaties

Elk netwerk – of het nu autoverkeer, brieven of bytes vervoert – wordt in de wiskunde voorgesteld door een graaf, een abstract ding dat bestaat uit een aantal knooppunten of knopen, en elke knoop kan verbonden zijn met een of meer andere knopen door een lijn (in het Engels heten die respectievelijk: vertex en edge). Als de graaf het Europese elektriciteitsnet voorstelt zijn de knopen elektriciteitscentrales en de lijnen hoogspanningsleidingen; als het een graaf is van Facebook, zijn de knopen Facebook-pagina’s en de lijnen Facebook-vriendschapsrelaties.

Traditioneel bestudeerden wiskundigen grafen met een klein aantal knopen, of grafen met een heel regelmatige structuur, bijvoorbeeld een ‘matje’ waarin elke knoop met zijn vier naaste buren verbonden is. Ook dan kan het heel moeilijk zijn om bepaalde eigenschappen van grafen te bewijzen, maar in ieder geval beschik je over alle relevante informatie.

Maar met deze aanpak kom je niet ver als je het Word Wide Web of Facebook wilt analyseren. Zulke netwerken zijn zo groot dat je geen volledige lijst met knooppunten en verbindingen kunt opstellen, te meer omdat ze voortdurend veranderen. Niemand weet hoeveel webpagina’s er online zijn, maar het zijn er zeker vele miljarden, en het aantal links tussen die pagina’s is nog veel groter.

Het beste model voor zulke complexe netwerken blijkt een random graaf te zijn, een netwerk waarin je (binnen bepaalde randvoorwaarden) willekeurige knopen met elkaar verbindt.

Hoewel zo’n netwerk op kleine schaal bekeken een chaos is, voldoet het op grote schaal toch aan interessante wetmatigheden. Neem bijvoorbeeld de vraag of een netwerk samenhangend is. Dat wil zeggen: kan je vanuit elk knooppunt via de verbindingen elk ander knooppunt bereiken? De theorie van random grafen zegt, dat er een omslagpunt ligt bij gemiddeld één verbinding per knooppunt. Is het aantal verbindingen minder dan 1, dan valt het netwerk als los zand uit elkaar. Is het aantal groter dan 1, dan zal het overgrote deel van het netwerk samenhangen (dit heet de reuzecomponent). De rest bestaat uit ‘stof’, een stel relatief piepkleine, onderling niet verbonden netwerkjes.

Hoe zit dat met Facebook? Iedereen mag zelf een Facebook-pagina beginnen, je hoeft Marc Zuckerberg er niet voor te kennen, of wie dan ook die al lid is van Facebook. Het is daarom denkbaar, dat Facebook had bestaan uit een groot aantal losse vriendennetwerkjes. Dat geldt bijvoorbeeld voor het denkbeeldige netwerk van leden van voetbalclubs: vrijwel niemand is lid van meer dan één voetbalclub, de meeste fanclubs zullen wat dat betreft eilandjes zijn.

Maar Facebook voldoet keurig aan de voorspelling voor een random graaf. Uit een groot onderzoek in 2011 bleek dat 99,91% van alle destijds 721 miljoen Facebook-gebruikers in de reuzecomponent zitten. Iets meer dan een half miljoen Facebookers vielen daar buiten. Het grootste netwerk in het ‘stof’ had maar tweeduizend leden, de rest was nog kleiner. Sindsdien is Facebook nog een stuk groter geworden; het heeft nu ruim een miljard gebruikers, maar de eigenschappen van zulke enorme netwerken veranderen niet of nauwelijks als ze groeien.

Reuzecomponent

Een andere wezenlijke vraag over een netwerk: is het een ‘kleine wereld’? Het concept van de kleine wereld werd bekend door de experimenten van Stanley Milgram in de jaren zestig. Die vroeg een paar honderd proefpersonen om een brief aan een hen onbekend persoon ergens in de VS te sturen, door hem te posten naar de vriend waarvan ze dachten dat die de beste kans maakte om de brief dichter bij de bedoelde persoon te brengen. De brieven die aankwamen – een minderheid – waren meestal vijf of zes keer doorgestuurd voor ze hun bestemming bereikten. Het idee, dat ieder mens op deze wereld via een stuk of vijf tussenpersonen ieder ander mens kent, is daarna in experimenten met e-mail bevestigd en gemeengoed geworden.

Facebook blijkt zelfs nog kleiner: iedereen in de reuzecomponent kan in ongeveer vier stappen elke andere Facebooker bereiken. Dus als jij op Facebook zit, zijn alle andere Facebookers minstens jouw Facebook-vriend-van-een-vriend-van-een-vriend-van-een-vriend.

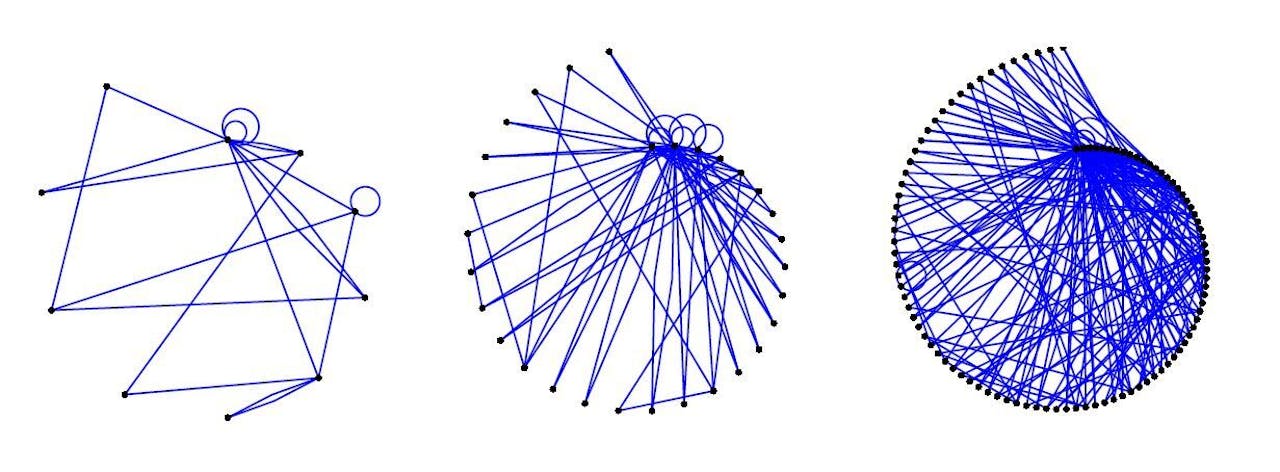
Een graaf die groeit, waarbij nieuwe knooppunten bij voorkeur verbindingen leggen met knooppunten die al relatief veel verbindingen hebben.
R. van der Hofstad

Het ‘kleine wereld’-fenomeen treedt niet op in een graaf waarin alle knopen ongeveer evenveel verbindingen hebben. Maar in een random graaf zullen sommige knopen toevallig veel meer verbindingen hebben dan gemiddeld. Die nemen dan automatisch de rol van hubs op zich, knooppunten waarlangs je snel andere delen van het netwerk bereikt. Dit is ook de reden voor de fameuze paradox, dat je vrienden gemiddeld meer vrienden hebben dan jijzelf.

Dit effect is nog sterker in een random graaf die groeit, waarbij je aanneemt dat nieuwe knopen bij voorkeur verbindingen leggen met ‘populaire’ knopen (die al relatief veel verbindingen hebben). Vertaald naar Facebook: hoe meer vrienden iemand al heeft, hoe groter de kans dat hij of zij er nog vrienden bij krijgt.

Dit zorgt voor een ‘de rijken worden rijker’-effect dat de onderlinge verschillen steeds groter maakt. Remco van der Hofstad van de Technische Universiteit Eindhoven onderzocht dit proces: “Eigenlijk is het niet ‘de rijken worden rijker’, maar ‘de ouden worden rijker.’” Immers, van degenen die er vroeg bij waren, bouwen sommigen een voorsprong op die daarna alleen maar steeds groter wordt. Zo blijkt het ‘kleine wereld’-fenomeen een bijna universele eigenschap van complexe netwerken; het heeft weinig te maken met bewuste beslissingen van individuen of de sociologie van de mensenmaatschappij.

Een dood dier besmet met Ebola wordt opgeruimd
Dr. Benard Ssebide

Epidemie effectiever bestrijden

Ook op de uitbraak van een ziekte als Ebola of vogelgriep kun je netwerkanalyse toepassen. Mensen of boerderijen vormen de knopen in het netwerk, en wie besmet raakt, is verbonden met een ander.

Hoewel de modellen op dit moment nog niet heel realistisch zijn, doemt ook hier het ‘kleine wereld’-effect op. Voor een epidemie houdt dit in dat deze vooral in stand gehouden wordt door hubs, een relatief klein aantal mensen die extreem veel contacten hebben. Als je die kan identificeren in de populatie, kun je de epidemie veel effectiever bestrijden dan door algemene maatregelen voor de hele bevolking door te voeren.

Volgens Michel Mandjes verkeren de diverse onderzoekslijnen binnen NETWORKS nog wel in een fundamentele fase. Hij verwacht dat deze wiskundige modellen en technieken pas over een paar jaar geschikt zijn om netwerken in de echte wereld beter te managen.

Reageer