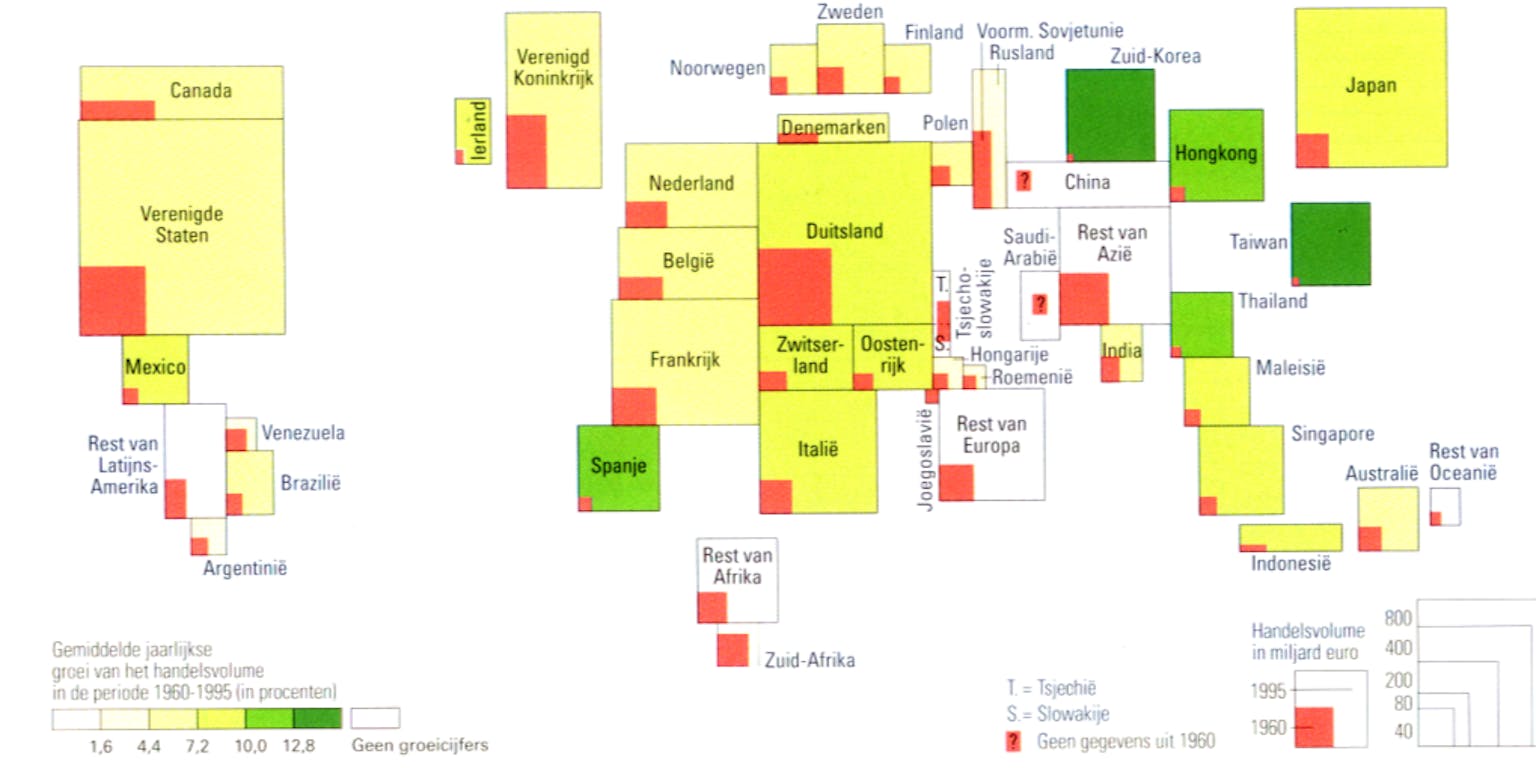
Landkaarten zijn vaak ook bruikbaar om andere dan geografische informatie mee te presenteren. Als alle landen worden teruggebracht tot rechthoeken, spreekt men van ‘rechthoekige cartogrammen’. Het is een vak apart om gegevens zodanig onder te brengen in een rechthoekig cartogram, dat de gebieden op de kaart herkenbaar blijven. Dan zie je bijvoorbeeld dat Nederland echt niet zo klein is in Europa.
Voor zover bekend was Erwin Raisz in 1934 de eerste die een rechthoekig cartogram gebruikte om data te visualiseren. Hij maakte toen een plaatje van de bevolking van de Verenigde Staten, waarbij elk hokje het bevolkingsaantal in een staat voorstelde. De grootte van het hokje gaf het inwoneraantal in miljoenen aan.
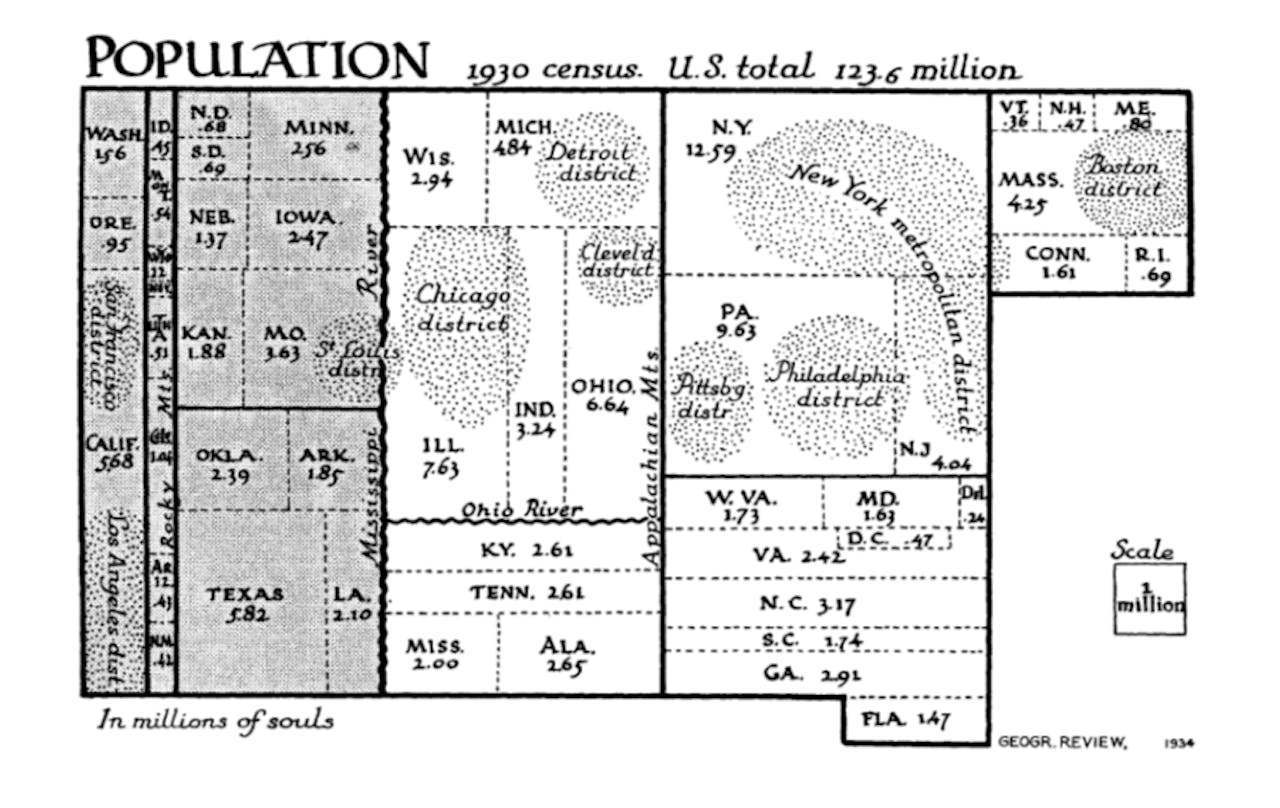
De geografische kaart van de Verenigde Staten is er nog wel in te herkennen: Californië ligt helemaal in het westen, New York in het oosten, en Florida in het zuid-oosten. Raisz puzzelde zijn cartogram met de hand in elkaar, maar hoe goed was zijn oplossing? Wat ís eigenlijk een goede oplossing? En als je dat ondubbelzinnig kan omschrijven, kun je dan een computer automatisch cartogrammen laten maken, met als input een landkaart en een setje data?
Droge humor
Dat is een van de kwesties die Bettina Speckmann, hoogleraar toegepaste geometrische algoritmes aan de TU Eindhoven, de afgelopen jaren heeft uitgezocht. Zij gaf de plenaire openingslezing op de Nationale Wiskunde Dagen (NWD), begin februari. Voor een zaal met honderden wiskundeleraren en wiskundigen, lardeerde Speckmann haar lezing met droge humor. Zo vertelde ze, dat ze in 2009 met dit onderwerp ook al op de NWD was, maar dan in een parallelsessie. “Toen hadden we nog helemaal niet door hoe de wiskundige structuur van die dingen is. Nu snappen we dat wel – en dan mag ik de plenaire lezing geven.”
Cartogrammen moet je niet verwarren met ingekleurde landkaarten, waarbij niet de oppervlakte, maar de kleur van een gebied de informatie moet overbrengen. Zulke ingekleurde kaarten wekken vaak verwarring. “Mensen integreren altijd de kleur over de oppervlakte.” De wiskundige term ‘integreren’ betekent hier, dat mensen onbewust letten op de totale hoeveelheid van een kleur, terwijl die in een ingekleurde landkaart vaak irrelevant is.
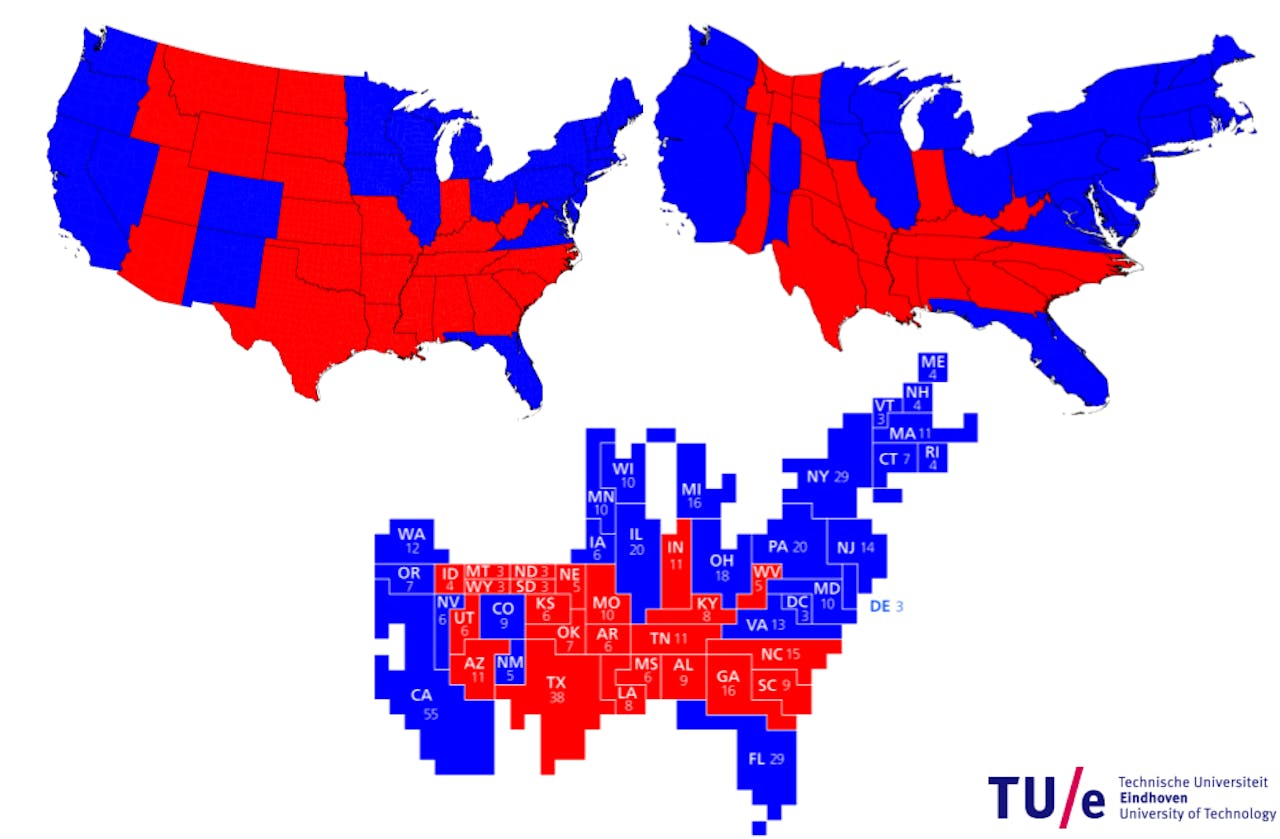
Linksboven: kaart van de Verenigde Staten, ingekleurd per staat met de verkiezingsuitslag. Rechtsboven: kaart vervormd, zodat de grootte van een staat het aantal kiesmannen aangeeft. Onder: deze inkleuring als rechthoekig cartogram.
B. SpeckmannEen voorbeeld is het bekende kaartje met de uitslag, per staat, van de presidentsverkiezing van 2012 in de VS. De geografische kaart is ingekleurd met rood (de Republikeinse kandidaat won) of blauw (de Democraat won), en maakt niet duidelijk waarom Barack Obama gewonnen heeft. De kaart is immers overwegend rood.
Pas als je de oppervlakte van elke staat evenredig maakt aan het aantal kiesmannen dat zo’n staat levert voor de formele stemming, zie je dat een flinke meerderheid ‘blauw’ stemde.
Een cartogram hoeft niet uit rechthoeken te bestaan, maar volgens Speckmann heeft zo’n simpele standaardvorm voordelen. “Mensen weten meteen dat je niet naar een echte kaart kijkt, en de oppervlakte van rechthoeken is goed in te schatten.”
Goede en slechte voorbeelden
Bij het maken van een rechthoekig cartogram is de keuzevrijheid enorm, maar je wilt natuurlijk, dat het resultaat nog te herkennen is als een kaart van een bepaald gebied. Dat leidt tot een paar criteria die voldoende conreet zijn om in een computerprogramma te zetten. Uiteraard moeten de rechthoeken de juiste oppervlakte hebben (voor het gegeven dat je wilt laten zien). Buren moeten buren blijven. De relatieve posities van de rechthoeken moeten ongeveer correct zijn. En, tot slot, de lengte-breedte verhouding mag niet te groot zijn.
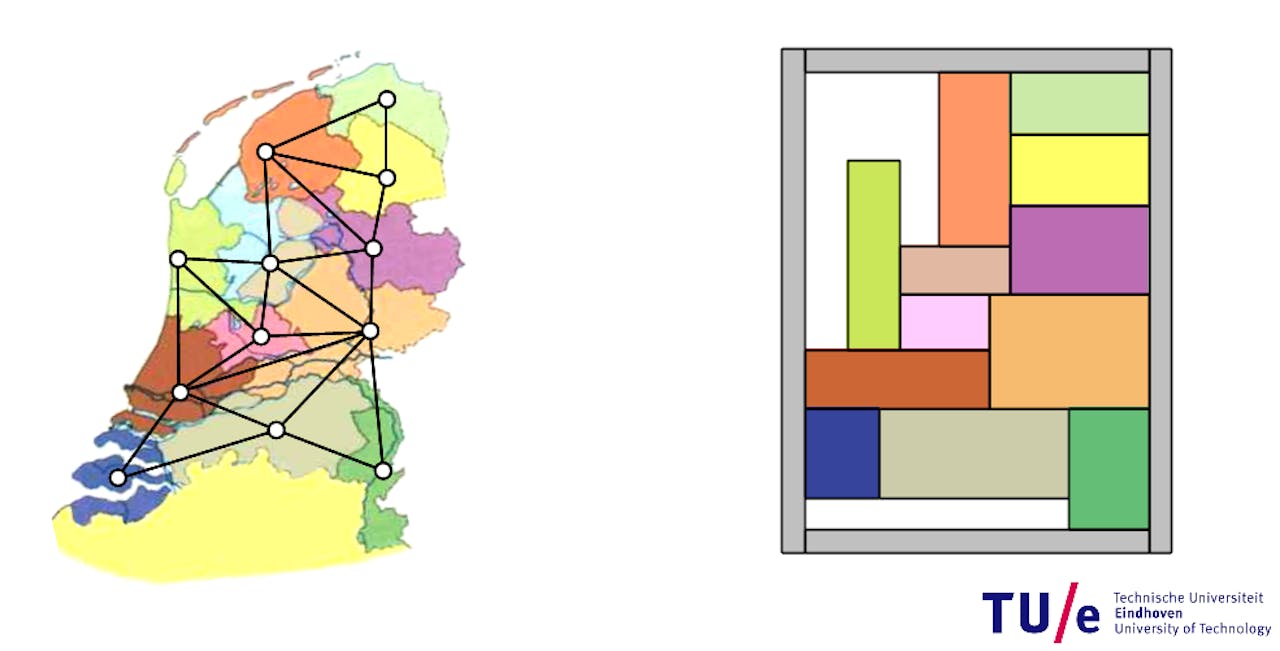
Links de Nederlandse provincies als graaf, rechts als rechthoekig cartogram.
B.SpeckmannWiskundig gezien is dit een probleem met vlakke grafen, waar al veel theorie over bekend is. Een graaf is, simpel gezegd, een netwerk van knooppunten. Een graaf kan van alles voorstellen (wiskundigen zeggen: ‘een graaf kan duaal zijn met’): treinstations en de spoorverbindingen daartussen, een familie met hun verwantschapsrelaties, of een setje getallen die al of niet een gemeenschappelijke deler hebben.
In het geval van de cartogrammen komt elk knooppunt overeen met een land of gebied, en een verbinding tussen twee knooppunten geeft aan dat die twee gebieden buren zijn. Verder heeft elke knoop een ‘gewicht’, de grootheid die je met je cartogram wilt weergeven. Voor een echte kaart is het gewicht gelijk aan de landoppervlakte, maar het kan dus ook het aantal inwoners zijn, of de export in miljarden euro’s, of het aantal gevallen van griep in dat gebied.
Het is meteen duidelijk, dat niet elke graaf te transformeren is tot een rechthoekig cartogram. Als een land wordt ingesloten door drie buren, kun je dit onmogelijk voorstellen met rechthoeken zonder buren van elkaar te scheiden. Zo kun je alleen rechthoekige cartogrammen van de Europese Unie maken, door Luxemburg weg te moffelen in België.
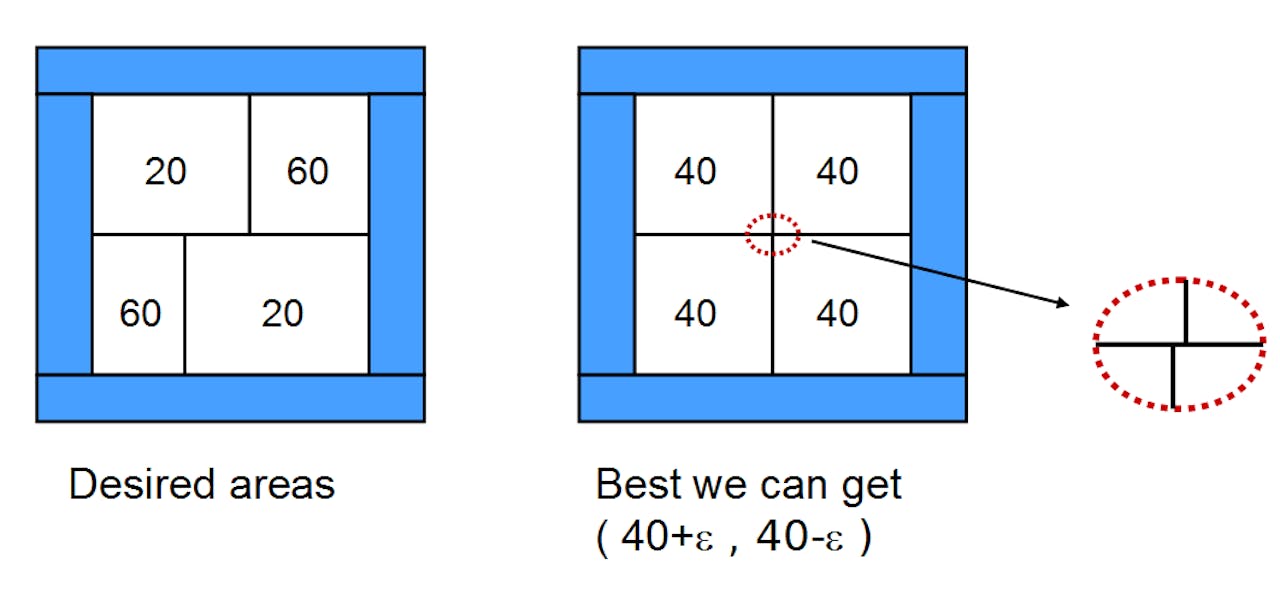
De nabuurrelaties tussen landen en de groottes die ze moeten krijgen in het cartogram, kunnen met elkaar in tegenspraak zijn.
B.SpeckmannOok zijn er combinaties van gewichten van naburige landen, die je niet met rechthoeken kunt weergeven zonder de buurrelaties aan te tasten (zie de illustratie hierboven). Als je zulke struikelblokken uitsluit, of toelaat dat je een beetje schippert met de buurrelaties, dan is het aantal mogelijke cartogrammen gigantisch.
Onoverzichtelijk veel
Onderzoek van Speckman en anderen toonde aan, dat het aantal mogelijke cartogrammen, afhankelijk van het aantal knooppunten n, tussen 3n en 4,68n ligt. Voor de Europese Unie, met 27 landen, is dat al een astronomisch aantal. Speckmann liet ooit een computer cartogrammen van de Europese Unie maken om het exacte aantal te achterhalen, maar dat was onbegonnen werk. “Na drie weken zijn we gestopt met tellen.” De teller stond toen op 1,3 miljard. Voor de hele wereld, met circa tweehonderd landen, is de situatie nog veel onoverzichtelijker.
Hoe vind je in die enorme variatie het beste cartogram? Je wilt natuurlijk, dat alle landen zoveel mogelijk op hun plek blijven en zoveel mogelijk de echte vorm benaderen. Dus Noorwegen toon je liever niet als vierkant, en Duitsland niet als een lange strook. Ook wil je, dat Noorwegen en Duitsland zoveel mogelijk de juiste onderlinge afstand hebben, en dat hun verbindingslijn ongeveer noordnoord-west loopt, net als in het echt. Daar zijn getalsmatige criteria voor te formuleren. Vaak kun je die flink verbeteren, als je afwijkingen van een paar procent in de oppervlakte toelaat. Een rechthoek die twee of drie procent kleiner is dan zou moeten, valt visueel immers niet op. Terwijl dat net voldoende kan zijn om de puzzel in elkaar te passen.
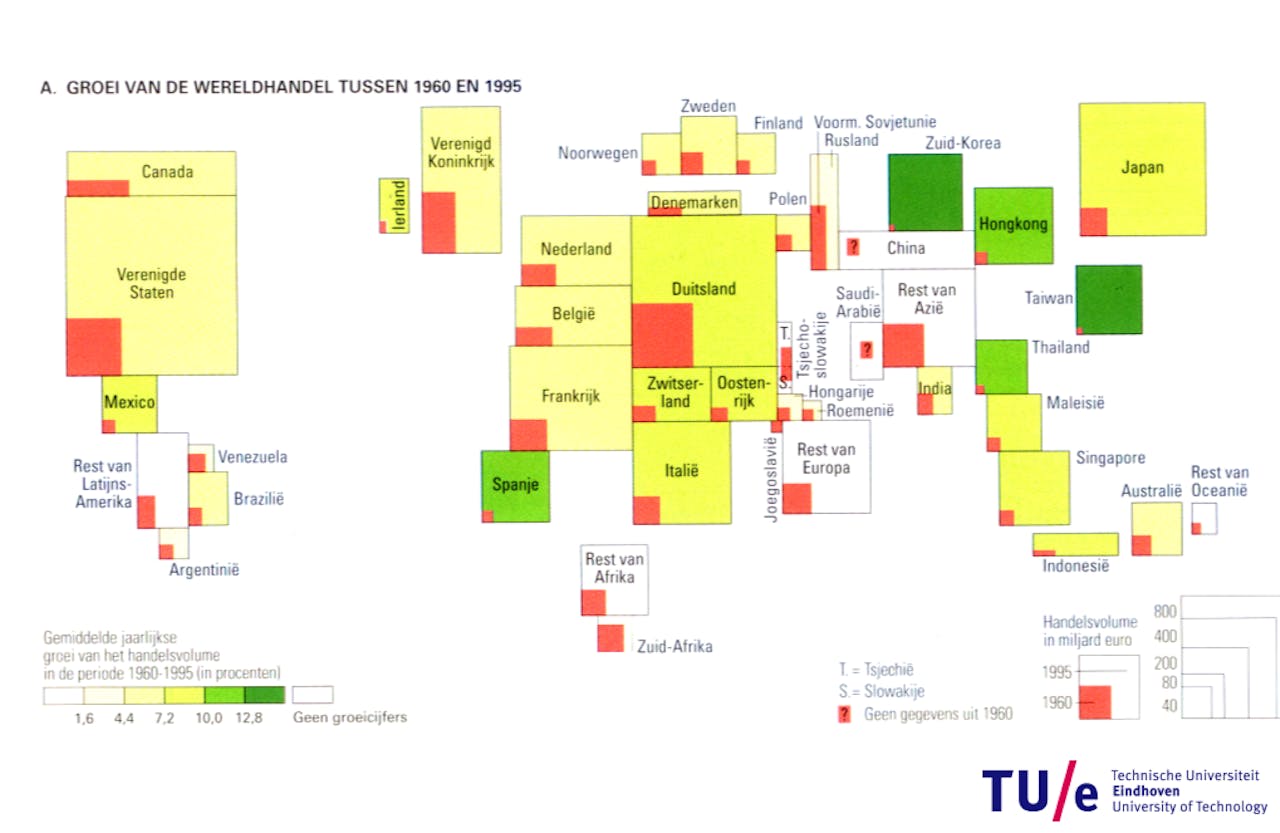
Groei van de internationale handel tussen 1960 en 1995. Uit het feit dat de Verenigde Staten hier ongeveer net zo groot is als Duitsland, kun je concluderen dat de export van de Verenigde Staten relatief gering is, vergeleken met de binnenlandse handel.
B.SpeckmannVanwege het enorme aantal mogelijke cartogrammen, is het ook voor een computer niet te doen om ze een voor een uit te proberen en de beste wat betreft die criteria te behouden. Speckmann ontdekte echter, dat je handig gebruik kunt maken van de eigenschappen van de duale graaf van de kaart waarvan we het cartogram willen maken. Alle mogelijke cartogrammen voor een kaart komen overeen met bepaalde inkleuringen van deze duale graaf (waarbij elke lijn een van twee kleuren krijgt).
Deze inkleuringen hebben een specifieke wiskundige structuur, een zogeheten ‘distributieve tralie’. Door die wiskundige structuur zijn alle mogelijke configuraties van rechthoeken goed te inventariseren.
Wat dan overblijft, is een type optimaliseringsprobleem dat vaak opduikt in de natuurwetenschappen, en waarvoor – voor zover bekend – geen onfeilbare en toch efficiënte oplossing bestaat. Maar er bestaan wel methodes die meestal vrij efficiënt een bijna optimale oplossing vinden. Speckmann: ‘En dat zou een stuk minder goed werken, als we die structuur van de distributieve tralie niet als basis hadden.’
De computer begint met willekeurig een flinke hoeveelheid cartogrammen te genereren, waarvan je op statistische gronden aanneemt, dat die bijna de complete variatie aan mogelijkheden bevat. Vervolgens begin je bij één willekeurige oplossing, en probeer je door kleine variaties in de lengte/breedteverhoudingen en de positie van de rechthoeken een iets betere, hoger scorende oplossing te vinden. Als dat lukt, ga je in die richting verder in de hoop op een nog hogere score.
Vroeg of laat kom je op zo’n pad door het denkbeeldige landschap van cartogrammen niet verder meer ‘omhoog’. Je hebt dan ofwel de hoogste top in het landschap gevonden, ofwel een locale top die niet het hoogste is. Daarom maak je af en toe, opnieuw bepaald door toeval, een grote sprong door het landschap, zodat je bij een heel ander cartogram opnieuw begint met een weg omhoog te volgen, hopelijk naar een hogere top. Uiteindelijk is ook de beslissing om niet langer door te gaan met zoeken min of meer een gok.
Dat levert bijvoorbeeld dit plaatje op van de wereldbevolking:
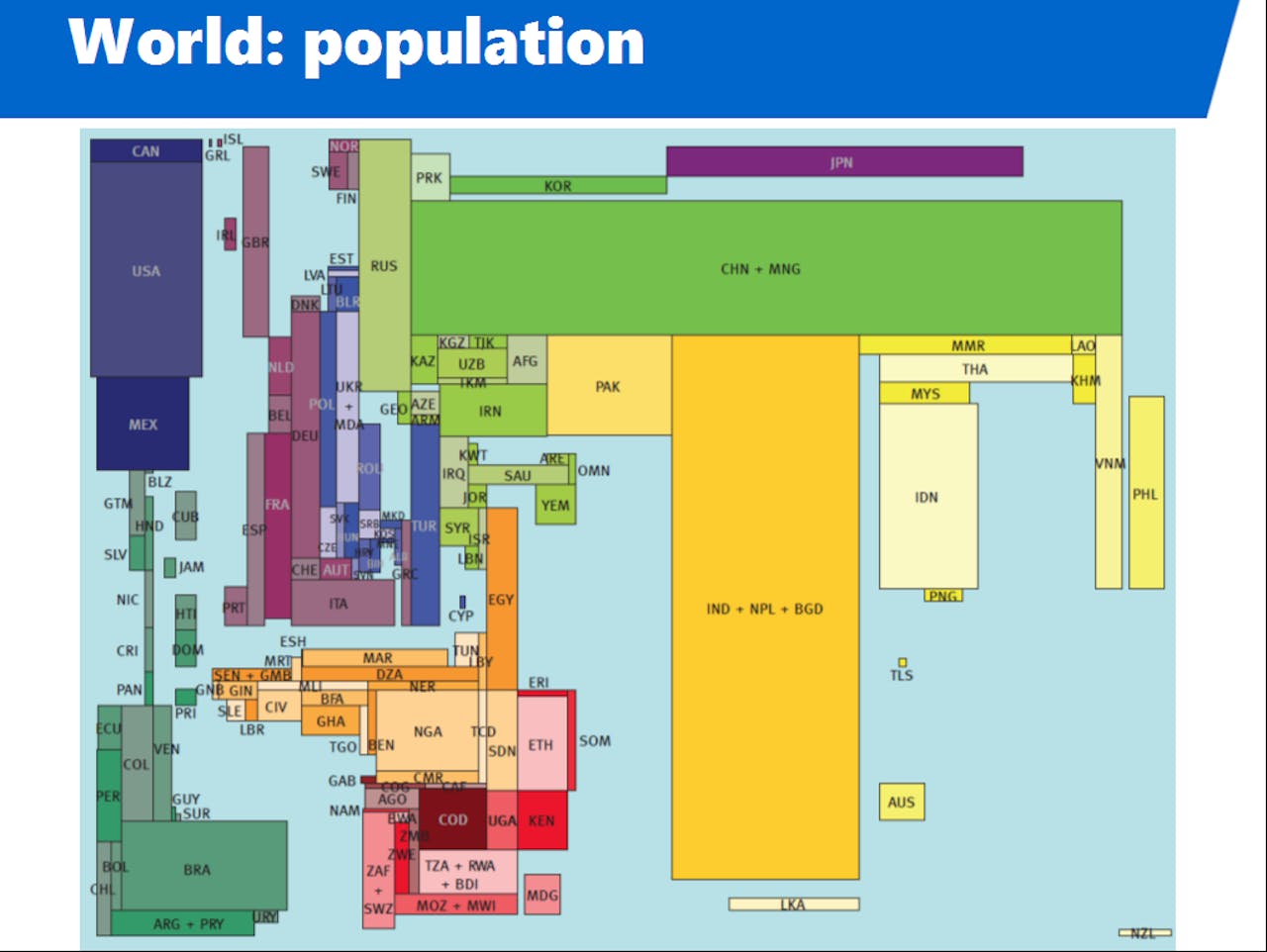
Cartogrammen kunnen je helpen om zaken in het juiste perspectief te zien. Zo spelen Nederlandse politici, als het om Europese politiek gaat, nogal eens de Calimero-kaart: ‘wij zijn maar zo klein in Europa, Nederland kan op eigen houtje niks veranderen’. Maar kijk nu eens naar het formaat van Nederland in Europa als het gaat om de waarde van de export:
Op Speckmanns webpagina kun je zelf cartogrammen maken , en het opnemen tegen de computer (ten tijde van het publiceren van dit artikel lag het online cartogrammenspel tijdelijk stil wegens onderhoud)