Als de zon erg laag staat voelt hij nauwelijks warm. De oorzaak daarvan is de verzwakking van de zonnestraling door de atmosfeer.
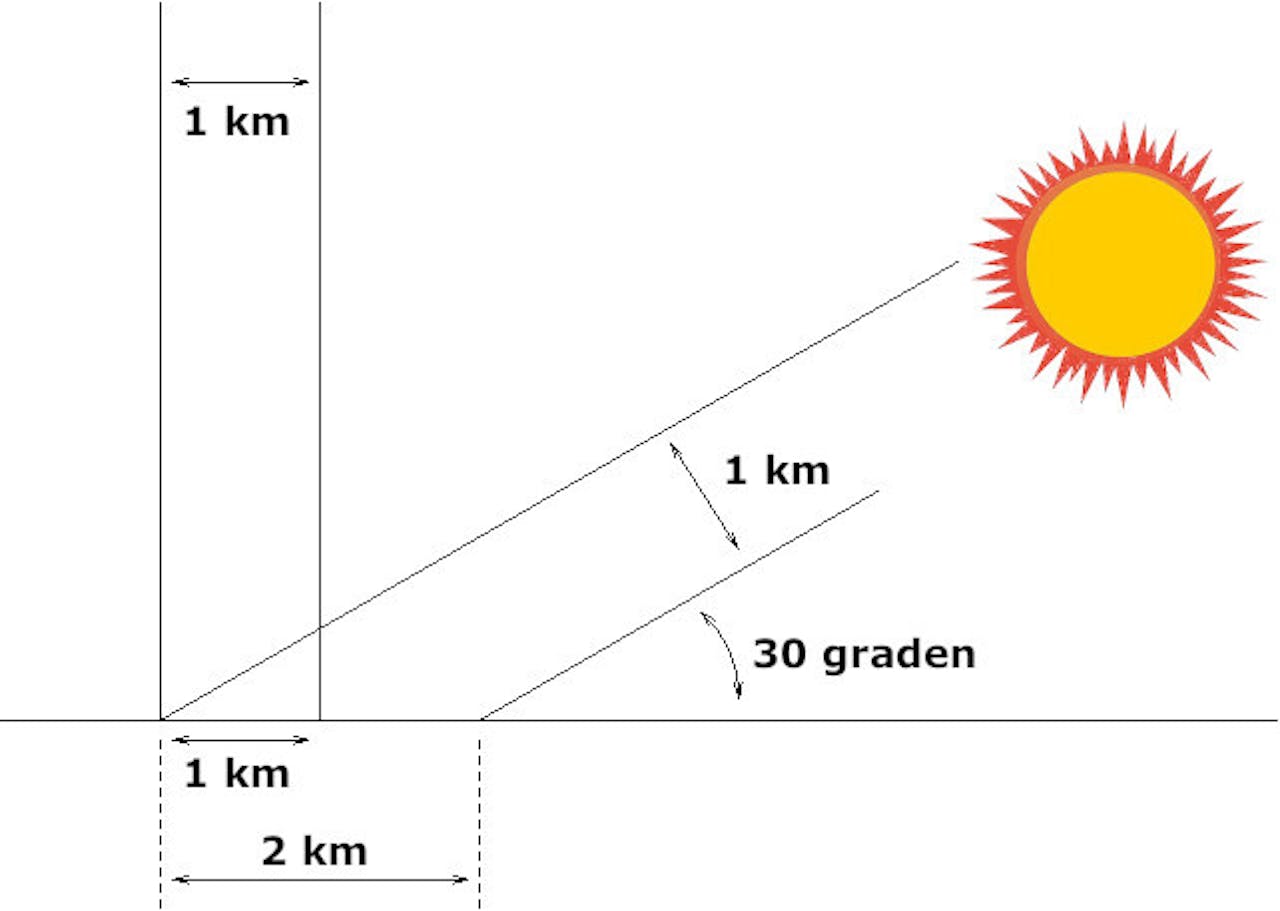
Als de zon laag staat, moet hij door een veel dikkere laag atmosfeer schijnen dan wanneer hij hoog staat. Dat wordt duidelijk als we bedenken dat die atmosfeer, relatief gezien, maar een dunne schil rond de aarde vormt: in verhouding minder dik dan een sinaasappelschil rond een sinaasappel. Een flink schuine inval maakt de weg door de atmosfeer heel wat langer, en de straling dus heel wat zwakker. Dat geldt met name voor het ultraviolette stuk van het zonnespectrum, waar onze huid bruin van wordt: de verzwakking daarvan door de atmosfeer is relatief groot, en een wat kortere of langere weg scheelt dan al gauw een slok op een borrel. We merken dat bijvoorbeeld als we wat hoger zitten, in de bergen. Daar is het UV extra sterk, en zonnebrand extra belangrijk. Kortom: voor dit soort zaken is het handig om te weten hoe hoog de zon komt.
Voor mensen die op de evenaar wonen is het makkelijk: op het midden van de dag staat de zon pal boven hun hoofd, althans op 21 maart en 21 september. Bij ons in Nederland, op ongeveer 52 graden Noorderbreedte, staat de zon 52 graden lager. Vanaf de horizon gemeten dus nog maar 90-52=38 graden hoog.
Maar doordat de aardas een beetje scheef staat komt daar, hartje zomer, nog 23,5 graad bij: de zon staat dan boven de noordelijke keerkring, de Kreefts-keerkring. Dat maakt dus 38 + 23,5 = 61,5 graad.
In de winter gaat hetzelfde bedrag eraf, en blijft er niet veel over: 38 – 23,5 = 14,5 graad.
figuur1
Hoe zit het daartussenin? Bij het bepalen hiervan hebben we een meevaller. We kunnen prachtig gebruik maken van het feit dat er ongeveer evenveel dagen zijn in het jaar (365) als er graden zijn in een cirkel (360). De aarde legt in zijn baan om de zon dus elke dag een afstand van ongeveer een graad af. Mooier wordt het nog als we werken in termen van maanden: dan is het per maand gemiddeld 360/12 = 30 graden, de ene maand een graadje meer, de andere een graadje minder, maar gemiddeld 30 graden.
Nu wordt het makkelijk. De hoogte die de zon bereikt is in goede benadering een sinusvormige slingerlijn rond dat gemiddelde van 38 graden, met maximale uitslagen naar boven en beneden van 23,5 graad. Dat is weergegeven in de figuur hieronder.
figuur 2
Nu bereikt een sinuscurve al bij een hoek van 30 graden (dus een maand) de helft van zijn maximale uitslag, en heeft hij de volgende 60 graden (twee maanden) nodig voor de andere helft. Conclusie: rond 21 april heeft de zon al de helft van de winst binnen, en komt hij op (afgerond) 38 + 12 = 50 graden boven de horizon. Pas rond 21 juni haalt hij zijn maximum hoogte: bijna 62 graden. Twee maanden later, rond 21 augustus, passeert hij weer de 50 graden, en een maand later is hij weer op 38. En dan gaat het hard omlaag.
Hoe hard gaat het eigenlijk in het steile stuk, rond 21 maart en 21 september? Een klein beetje wiskunde levert 0,4 graad per dag; dat is dus per dag bijna de diameter van de zon zelf (die is vrij precies 0,5 graad). Daarentegen duurt het midden zomer en midden winter, rond 21 juni en 21 december, natuurlijk lang voor er een merkbaar verschil is. Gerekend vanaf de 21e blijken we hier ongeveer 12 dagen te moeten wachten voordat we een verschil vinden ter grootte van de zonnediameter.
Natuurlijk hebben we de zaken hier en daar een beetje vereenvoudigd. Zo hebben we de baan van de aarde om de zon voorgesteld als een cirkel, wat niet helemaal klopt: in werkelijkheid is de baan een ellips, en loopt de aarde wat harder in de winter (wanneer de afstand tot de zon iets kleiner is), en wat langzamer in de zomer (wanneer de afstand iets groter is). Daardoor zit er wat speling in die “21e”, en daardoor is ook de schijnbare zonnediameter niet constant. Bovendien is een jaar niet precies 365 dagen, maar 365 1/4 dag, zodat we af en toe een schrikkeljaar moeten inlassen om niet uit de pas te raken. Daardoor verspringt die “21e” af en toe nog wat extra. Maar alles bij elkaar genomen zijn onze uitkomsten toch vrij nauwkeurig.
Tot zover Nederland. Als we naar het zuiden reizen komt de zon natuurlijk ook hoger, en wel ruwweg een graad voor elke 100 km zuidwaarts. Dat is makkelijk in te zien. De omtrek van de aarde is 40 000 km, dus de afstand van de pool tot de evenaar 10 000 km. Dat correspondeert met 90 graden, en 10 000/90 levert 111 km, om precies te zijn. Kortom: als we naar de Riviera rijden, hebben we de zon al bijna 10 graden hoger dan in Nederland. In de winter betekent dat – afgerond – geen 15 maar 25 graden boven de horizon, midden op de dag. En dat is goed te merken.
Ten slotte: hoeveel scheelt het eigenlijk als we, behalve naar het Zuiden, ook nog naar de bergen gaan, de hoogte in? De zon komt daardoor niet hoger boven de horizon, maar wordt wél feller, omdat de straling door een dunnere laag van de atmosfeer gaat. Het antwoord op deze vraag hangt van het seizoen af. Midden in de winter blijkt dat klimmen relatief weinig uit te maken. Neem bijvoorbeeld skieën in de Alpen, op zo’n 46 à 47 graden Noorderbreedte. Als we dat rond Kerst doen, als de Nederlandse zon waterig dun en laag boven de horizon staat, maakt de reis naar het Zuiden het meeste verschil: Zodra de zon dan iets hoger komt, neemt de laag atmosfeer waar hij doorheen moet behoorlijk af (met meer dan 25%, in dit geval), en wordt de straling al flink wat feller. Het stijgen naar 1000 meter (waar we zo’n 12% van de atmosfeer achter ons hebben gelaten) is dan nog maar een toegift.
In de winter valt zonlicht veel schuiner op de aarde dan in de zomer.
Wikimedia commons, Michael Hardy & Decefalus via CC BY-SA 4.0 / Roel van der Heijden
