Het patroon van plooien in een gekromd oppervlak onder krimpstress kan diverse patronen aannemen. Dit verschijnsel is nu pas wiskundig begrepen en experimenteel getoetst. Mogelijk helpt dit bij de fabricage van microstructuren, en geeft het nieuw inzicht in hoe embryo’s en kleine organismes zich ontwikkelen.
Men neme een hol bolletje van zacht plastic, bekleed met een dunne schil van harder plastic. Als je lucht uit het bolletje zuigt, krimpt de bol. Het oppervlak komt dan onder druk te staan en gaat plooien.
Schil
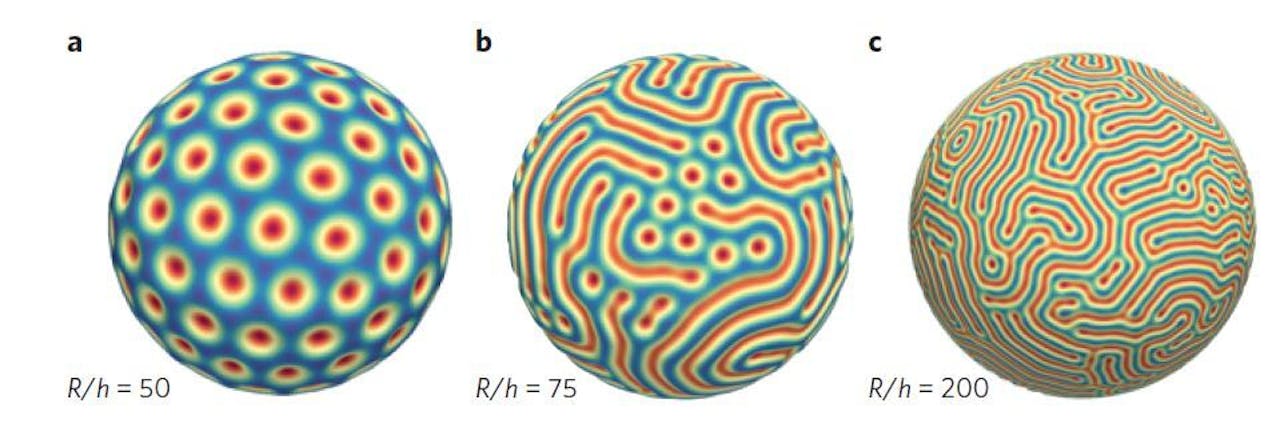
Dit is een voorbeeld van zogeheten spontane symmetriebreking. Je begint met een volkomen symmetrische situatie (het bolletje en de schil zijn homogeen, glad en bolvormig), maar ooit moet ergens de eerste plooi ontstaan, en die doorbreekt de perfecte bolsymmetrie. In de praktijk blijkt het patroon dat ontstaat afhankelijk van de relatieve dikte van de schil. Als de schil dik is, ontstaat een bijna regelmatig patroon van zeshoekige putjes (a). Bijna regelmatig, want het is onmogelijk om een bol naadloos te overdekken met alleen zeshoeken, er zitten ook vijf- en zevenhoeken tussen. Dit volgt uit een stelling die de wiskundige Leonard Euler al in de achttiende eeuw bewees.
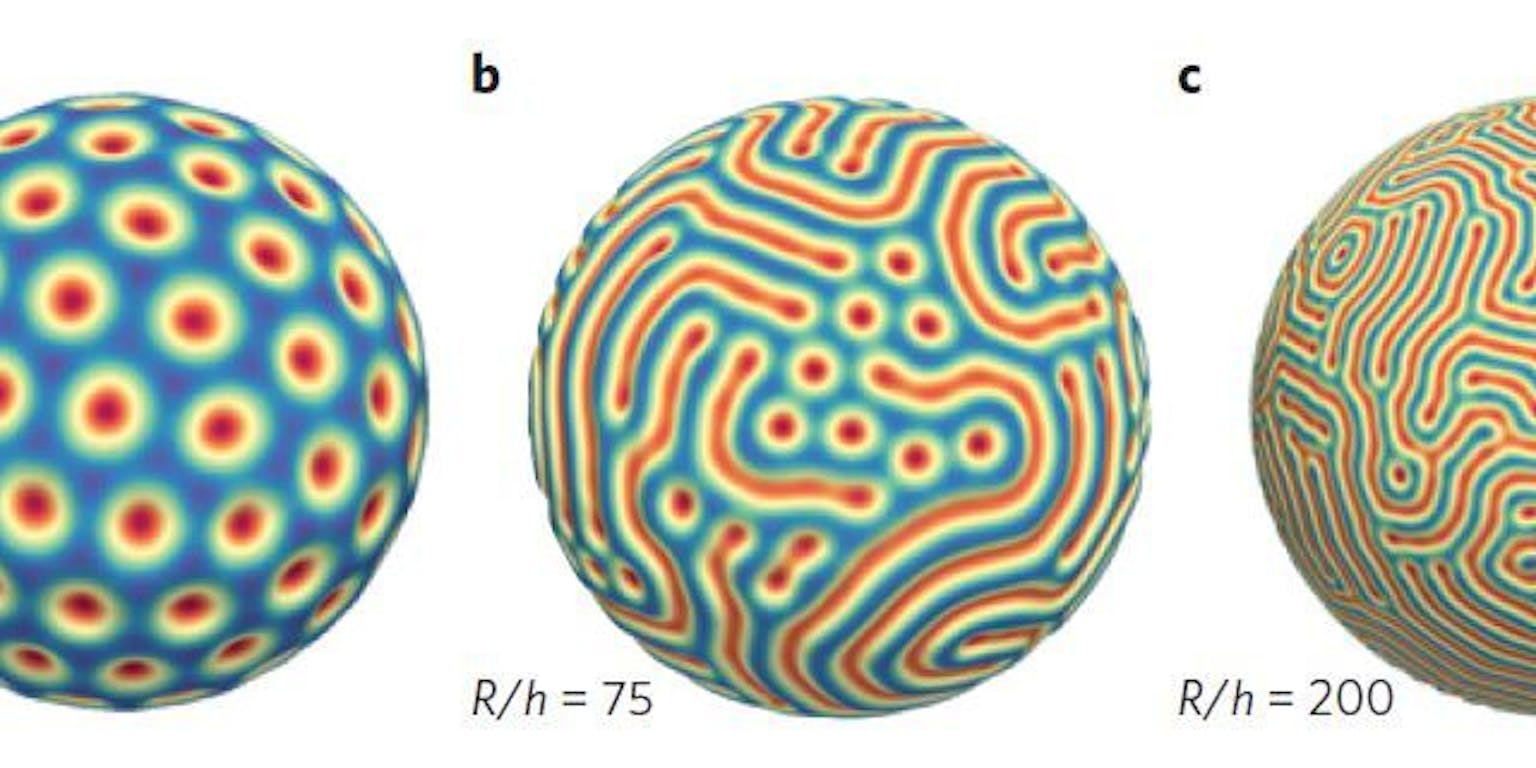
Rood is indeuking, blauw is ophoging. R is de straal van de bol, h de dikte van de schil.
Nature MaterialsMet een middelmatig dunne schil ontstaat een gemengd patroon, met valleien tussen de putjes (b). Als de schil dun genoeg is, kies het bolletje voor een doolhofpatroon, waarin alle putjes verdwenen zijn en het oppervlak geheel overdekt is met een toevallig patroon van valleien ©.
Theorie en praktijk
Natuurkundigen van het Massachusetts Institute of Technology (MIT) berekenden bovenstaande plooïingspatronen door een ingewikkelde differentiaalvergelijking op te lossen, voor zover mogelijk (er waren wat simplificaties nodig). Zo’n differentiaalvergelijking beschrijft voor elk minuscuul stukje schil welke trek- en duwkrachten er werken. Waardoor dat stukje vervormt en zelf ook weer tegen naburige stukjes schil gaat duwen of er aan trekt. De kunst is dan, om een stabiele oplossing te vinden waar alle krachten op elk punt van de schil met elkaar in evenwicht zijn. Een belangrijke randvoorwaarde is dat de schil nergens scheurt, want dan geldt de vergelijking niet meer.
Uiteraard volgde na de theorie de praktijk. Onderzoekers van MIT maakten zachte bolletjes van een paar centimeter doorsnede met een harde schil in diverse diktes, en zogen daar lucht uit. Het resultaat, gepubliceerd in Nature Materials, komt prachtig overeen met de berekeningen:

Slappe bol
Opmerkelijk genoeg hangen de resultaten alleen af van de relatieve dikte van de schil. En dus niet van de grootte van de bol of, binnen ruime grenzen, de materiaaleigenschappen. Een slappe bol met een keiharde schil vertoont hetzelfde plooiïngspatroon als een stugge bol met een matig harde schil. Als bewijs dat het formaat niet uitmaakt, vervaardigden ze ook bolletjes van maar een millimeter:

Ook werkt hun wiskundige methode voor willekeurige gekromde oppervlakken. Als voorbeeld berekenden ze het plooiïngspatroon van een torus (de relatieve dikte van de schil neemt van links naar rechts af):

Mogelijk is dit proces bruikbaar bij het efficiënt bouwen van bepaalde microstructuren. De onderzoekers denken ook, dat soortgelijke processen een rol kunnen spelen bij de groei van levende wezens. Elk embryo, bijvoorbeeld, begint als een bolletje cellen, waarna zich instulpingen vormen die later uitgroeien tot hele lichaamsdelen. De patronen doen ook denken aan de vlekken en strepen in de vacht van zoogdieren, en aan de bolsymmetrische vormen van sommige soorten plankton.