Wat is meer waard, de 100 meter horden in 13 seconden of 1 meter 80 hoogspringen? Het bepalen van een totaalscore voor ongelijksoortige prestaties is een interessant wiskundig probleem, onder meer bij de zevenkamp en de tienkamp in de atletiek. Scholieres Carine Candel en Hanna Knotnerus maakten hierover een profielwerkstuk dat een van de KNAW-onderwijsprijzen won.

Carine Candel en Hanna Knotnerus pleiten in hun winnende profielwerkstuk voor een statistisch verantwoorde puntentelling bij de zevenkamp die rekening houdt met de spreiding in de uitslagen. Hun complete werkstuk vind je hier
KNAWIn hun profielwerkstuk ‘Wiskunde, de achtste discipline in de heptatlon’, gaan Carine Candel en Hanna Knotnerus van het Montessori Lyceum in Amsterdam eerst de geschiedenis na van de puntentelling van de zevenkamp (vrouwen) en tienkamp (mannen) in de atletiek. Oorspronkelijk, begin 20e eeuw, was die telling gebaseerd op de Olympische records op de afzonderlijke onderdelen. De schaal begon bij een zekere minimale prestatie (0 punten) en liep tot 1000 punten bij evenaring van het Olympisch record.
Inmiddels overtreffen de huidige top-zevenkampsters op elk onderdeel de Olympische records van de toenmalige specialistes, zodat ze ver boven de 7000 punten zouden scoren (in feite staat het wereldrecord al sinds 1988 op naam van Jackie Joyner met 7291 punten). Je zou natuurlijk de schaal telkens kunnen aanpassen door de grens van 1000 punten bij het actuele Olympische record te leggen. Maar dan is het probleem dat je actuele uitslagen niet meer kunt vergelijken met oudere.
Sleutelen aan formules
Vanaf de jaren vijftig is daarom herhaaldelijk gesleuteld aan formules die een gelopen tijd of geworpen of gesprongen afstand omzetten in een aantal punten. Een belangrijke eis was dat de formules puntenaantallen opleverden die, in de overgangsfase, vrij nauwkeurig overeen kwamen prestaties in het oude systeem. Ook was een discussiepunt of de formules progressief moesten zijn, en zo ja, voor welke onderdelen? Progressief wil zeggen: een kleine prestatieverbetering levert meer extra punten op, naarmate de oorspronkelijke prestatie beter was. Dus een verbetering van 13,2 seconden naar 13,0 op de 100 meter horden moet meer extra punten opleveren dan een verbetering van 15,2 naar 15,0.
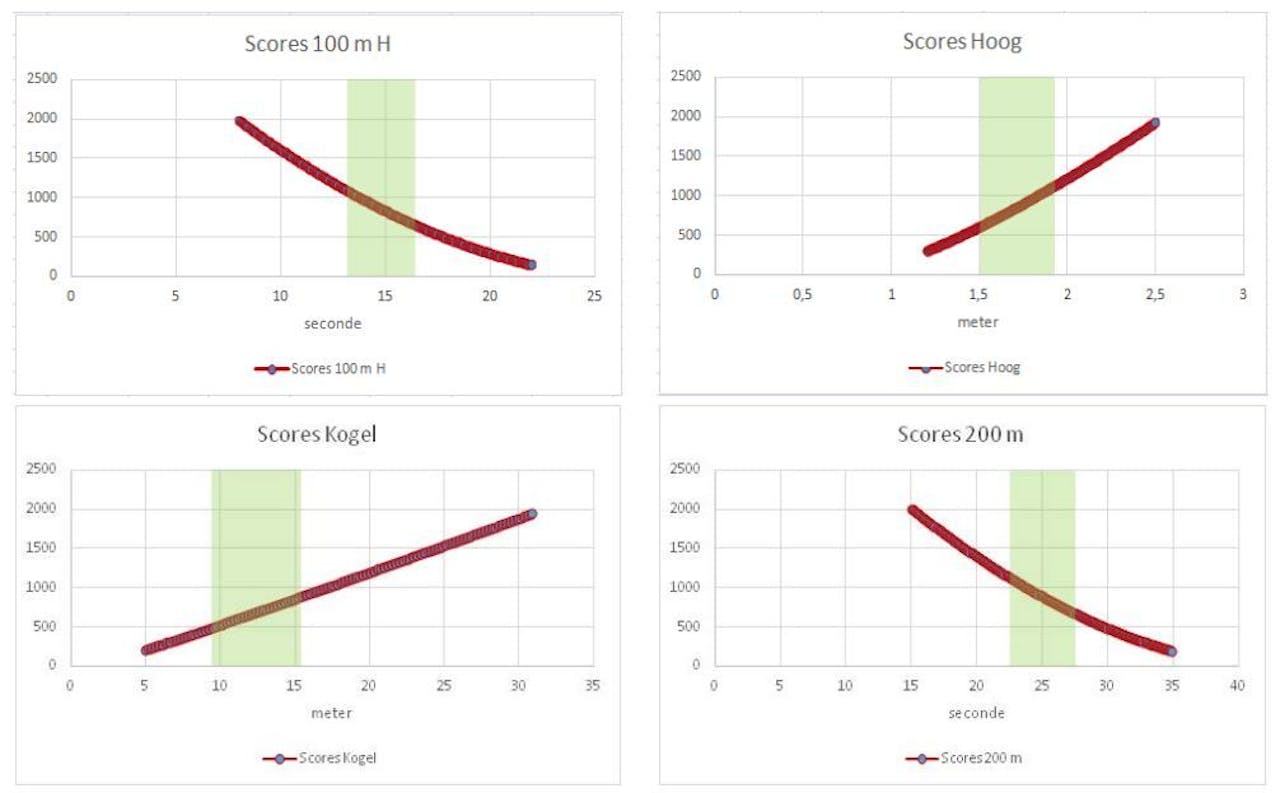
Grafiek van het verband tussen prestatie en aantal punten op vier onderdelen van de zevenkamp volgens de officiële puntentelling van de atletiekfederatie IAAF (‘100 m H’ is hordenlopen, ‘hoog’ is hoogspringen). De gekleurde band geeft de prestaties aan van de deelneemsters in de dataset die Candel en Knotnerus gebruikten om hun nieuwe puntensysteem te ijken. Het exacte puntenaantal wordt berekend uit een formule die voor elk onderdeel van de zevenkamp verschillend is.
KNAWOp grond van onduidelijke fysische overwegingen is destijds besloten, dat de puntentelling voor de loopnummers vrij sterk progressief moest zijn, die voor de springnummers minder, en die voor de werpnummers bijna niet. Na diverse wijzigingen zijn pas vanaf 1984 steeds dezelfde zeven formules gehanteerd – een voor elk onderdeel – zodat puntenaantallen vanaf die tijd echt vergelijkbaar zijn. De ‘progressiviteit’ van de formule wordt bepaald door de grootte van de exponent op het eind. Zo is de formule voor de 100 meter horden: 9,23076 × (26,7 – tijd in seconden)1,835. Een tijd van 14 seconden levert aldus (afgerond op hele punten) 978 punten op. Bij het kogelstoten is de formule: 56,02111 x (afstand in meters – 1,5)1,05. Een worp van 15 meter levert aldus 861 punten op.
‘Eerlijke’ puntentelling
Er is eigenlijk geen rechtvaardiging voor het feit dat de exponenten bij de loopnummers veel groter zijn. Het betekent dat je met 1 procent verbetering van je tijd op de 100 meter horden ongeveer 1,8 keer zoveel punten erbij verdient als met een 1 procent grotere afstand bij het kogelstoten of speerwerpen. Maar wat is dan wel een eerlijke weging van ongelijksoortige prestaties? Candel en Knotnerus geven zelf deze definitie: “Voor elk onderdeel moet het even moeilijk zijn om een bepaald puntenniveau te halen en om vervolgens eenzelfde aantal punten hoger te halen.” Maar hoe meet je dat?

Postzegel ter ere van Jackie Joyners wereldrecord op de zevenkamp in 1988, dat nog altijd stand houdt. Tijdens deze zevenkamp presteerde Joyner op vrijwel elk onderdeel beter dan de gespecialiseerde wereldrecordhoudsters tot 1950. Alleen met speerwerpen was ze ‘slechts’ beter dan de wereldrecordhoudsters tot 1932.
wikipediaAls maat voor hoe moeilijk het is om tot hogere prestaties te komen, kiezen ze voor een beproefde statistische methode: bepaal van een groot aantal deelnemers aan zevenkampen de gemiddelde prestatie per onderdeel, en de gemiddelde afwijking van dat gemiddelde (de standaarddeviatie of spreiding). Als er zeer veel spreiding in de prestaties zit, is er blijkbaar veel ruimte voor sporters om zich te verbeteren. Scoren alle deelnemers bijna dezelfde tijd (of afstand), dan is het blijkbaar heel moeilijk om boven de rest uit te steken, en mag elke minieme verbetering relatief veel punten waard zijn.
Dat leidt tot een puntentelling waarbij Candel en Knotnerus op elk onderdeel de gemiddelde prestatie 800 punten geven, en je 100 punten erbij verdient als je prestatie één standaarddeviatie beter is, en 100 minder als je één standaarddeviatie slechter bent. Daar tussenin krijg je punten naar evenredigheid.
In hun dataset van alle Nederlandse zevenkampsters die ooit meer dan 5000 punten hebben gescoord, is bijvoorbeeld de gemiddelde prestatie bij het hoogspringen 1 meter 73, met een standaarddeviatie van 6,4 centimeter. Dus als je 1 meter 73 springt scoor je 800 punten, en voor elke centimeter hoger krijg je er 100/6,4 = 15,625 punten bij.
Op deze manier worden alle onderdelen gelijk behandeld, mits een paar heel gebruikelijke statistische aannames kloppen (namelijk, dat de prestaties op alle onderdelen ongeveer ‘normaal’ verdeeld zijn). Het voordeel is ook, dat je alle kwantitatief meetbare sportprestaties op in principe dezelfde manier met elkaar kunt combineren (voor spelsporten als tennis of schaken moet je toch iets anders verzinnen).

Volgens de oude puntentelling heeft een prestatie op de 5000 meter een onevenredig groot aandeel in de eindoverwinning van de meerkamp: een verlies op de 500 meter is relatief makkelijk te compenseren door op de 5000 een stuk sneller te rijden. Mogelijk verklaart dat mede de jarenlange oppermacht van Sven Kramer bij de allround-toernooien: de 5000 meter is zijn sterkste afstand.
Bjarte HetlandDe schaatsmeerkamp
De aanpak van Candel en Knotnerus zou ook in andere sporten nuttig kunnen zijn. Zo geldt voor de klassieke vierkamp op het schaatsen (500, 1500, 5000 en 10.000 meter) nog steeds een simplistisch systeem waarin alle tijden worden teruggerekend naar de 500 meter en opgeteld. 0,3 seconde winst op de 500 meter vertaalt zich dus in een virtuele voorsprong van 3 seconden op de 5000 meter.
Is dit misschien meer door geluk dan wijsheid een eerlijk systeem? Dit zou het geval zijn, als de relatieve spreiding in de prestaties op elke afstand ongeveer hetzelfde is. Bij de EK in 2014 lag de gemiddelde tijd op de 500 meter rond de 37 seconden, met een spreiding van ongeveer een halve seconde, dus een relatieve spreiding van ongeveer 0,5/37 = 0,0135.
Op diezelfde EK was de gemiddelde tijd op de 5000 meter rond de 6 minuut 35 (395 seconden). Als je wilt dat de spreiding relatief even groot is, moet die rond de 0,0135 × 395 ~ 5 seconden liggen. In feite is de spreiding in de uitslagen van de 5000 meter eerder rond de tien seconden, en het verschil tussen de snelste en langzaamste rijder was bijna een minuut. Vertaald naar de 500 meter is dat een verschil van 6 seconden, veel groter dan in feite voorkomt op serieuze toernooien. Ook dat bevestigt het beeld, dat de relatieve spreiding in de uitslagen op de 5000 groter is dan op de 500.
Zo bekeken heeft de prestatie op de 5000 meter een onevenredig groot aandeel in de eindoverwinning: een verlies op de 500 meter is relatief makkelijk te compenseren door op de 5000 een stuk sneller te rijden. Mogelijk verklaart dat mede de jarenlange oppermacht van Sven Kramer bij de allround-toernooien: de 5000 meter is zijn sterkste afstand (op de 10.000 meter is het beeld vertekend, omdat die alleen door de acht besten van het klassement gereden wordt). Als een grondigere analyse van de uitslagen op alle WK’s en EK’s allround van de afgelopen jaren dit beeld bevestigt, zou de internationale schaatsunie serieus kunnen overwegen om ook op de schaatsvierkamp de door Candel en Knotnerus beschreven puntentelling in te voeren.

