Een Amerikaanse wiskundige bekeek een enorme hoop informatie over steden om zo formules af te leiden voor elk aspect van een stad: aan de hand van het inwonersaantal zijn dingen als verstopping van het verkeer, gemiddelde intelligentie, aantal uitvindingen per vierkante meter en meer nauwkeurig te voorspellen.
Als je wel eens met de auto door een grote stad zoals Amsterdam of Rotterdam hebt gereden, weet je het vast wel: er is altijd file. Het verkeer rijdt stapvoets, probeert fietsers en voetgangers te ontwijken en moet dan ook nog eens rekening houden met de talloze trams, bussen en treinen die langszoeven. Vervelend, als je snel ergens wilt komen.

De stad New York, in zwart-wit
Gottscho-Schleisner Collection, Library of CongressMaar voor de stad zelf is het een zegen. Steden waar de infrastructuur moeizaam is, zijn namelijk socialer en inventiever. Dat is in ieder geval één van de dingen die Luís Bettencourt van het Santa Fe-instituut in de Verenigde Staten ontdekte, door gegevens van grote en kleinere steden te vergelijken. Hij zag dat de meeste eigenschappen van steden eigenlijk hele simpele formules volgen: machtsfuncties van de vorm axb, waarbij a en b vaste waarden zijn. Zo kan je voor elk aspect van een stad een formule maken, door goede waarden voor a en b te kiezen.
Toekomstvoorspellen
Het is niet voor het eerst dat een stad wiskundig beschreven wordt. Omdat steden steeds groter en ingewikkelder worden, proberen velen om de stad in een meetbare vorm te gieten. Als je immers weet hoe de stad werkt, kan je ook voorspellen hoe hij gaat groeien en daar rekening mee houden tijdens het plannen van nieuwe wijken of grote verbouwingen.
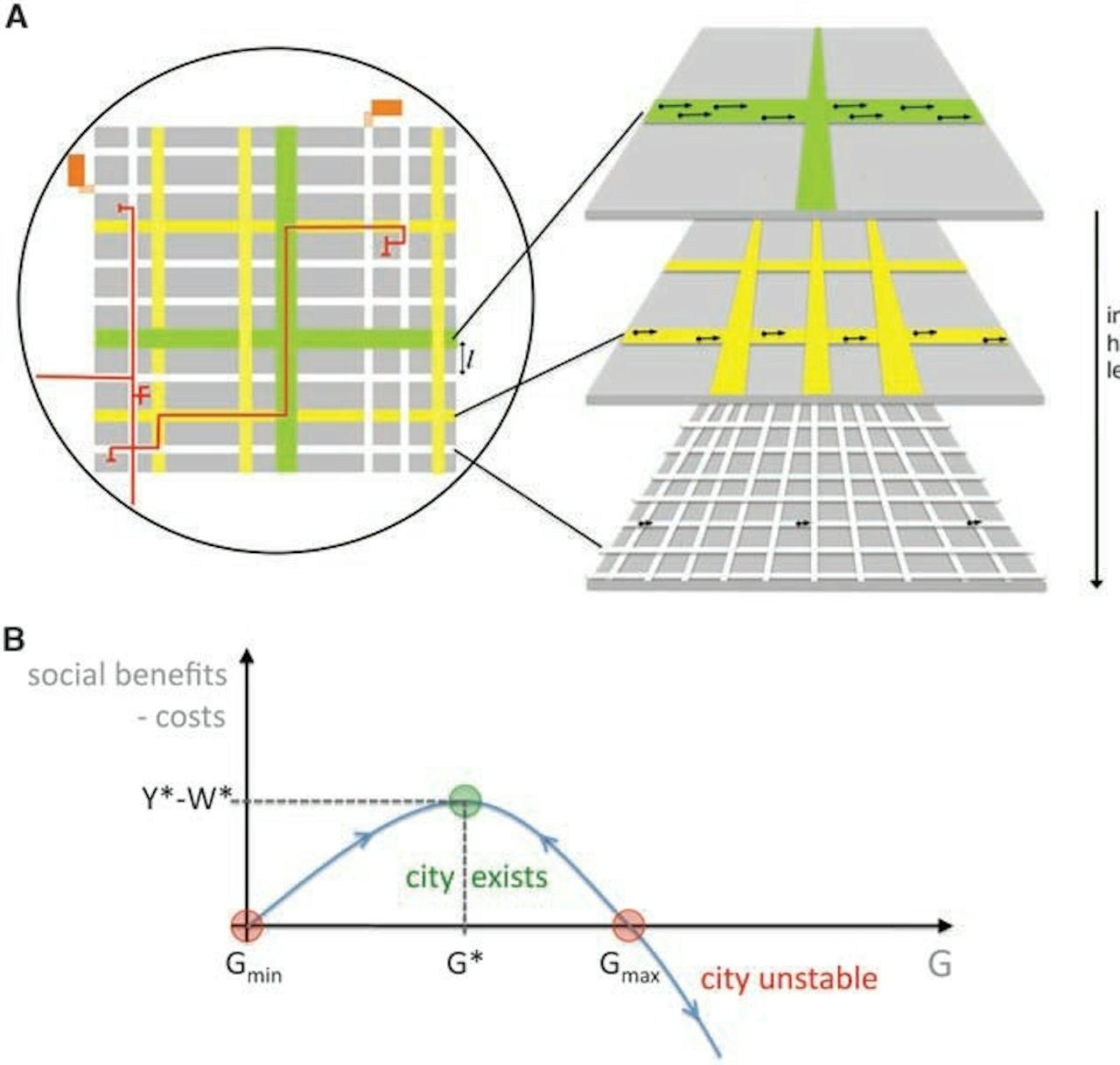
Visualisatie van hoe Bettencourts model een stad versimpeld. De grijze stukken staan voor bebouwing. De witte, groene en gele banen stellen de infrastructuur voor. Onder: een grafiek die de kosten van sociale contacten in de stad uitzet tegen de verbondenheid. In de grafiek is de zien dat er een balans tussen kosten en verbondenheid is waarin een stad kan bestaan.
Luís BettencourtMaar, zo meent Bettencourt in zijn paper dat afgelopen maand in Science verscheen, al die modellen waren vaak ontzettend ingewikkeld. Dat kwam omdat ze probeerden steden te modelleren zoals andere ingewikkelde structuren, zoals rivierdelta’s of ecosystemen. Nergens voor nodig, denkt de wiskundige van het Sante Fe-instituut in de Verenigde Staten. Als je gewoon kijkt naar alle informatie die steden toch al verzamelen, zie je dat bijna elke stad eenzelfde groei doormaakt en dat dingen als innovatie, infrastructuur en verbondenheid allemaal samenhangt met het inwonersaantal.
Kloppende formules
Bettencourt kwam op de formules door naar vele steden te kijken, waaronder Berlijn, New York en Peking. Eén van de formules, voor het aantal vierkante meters bestrating in een stad, klopte zelfs voor álle steden met meer dan 100.000 inwoners.
Voorlopig waagt hij zich echter nog niet aan toekomstvoorspellingen. Eerst moet het model nóg beter worden door bij meer steden te kijken of de formule’s kloppen. Daarna kan het misschien gebruikt worden door stadsplanners.

