Hardnekkig getalprobleem Booleaanse Pythagoreïsche Drietallenprobleem eindelijk opgelost, grens ligt bij 7824

Een supercomputer heeft het ‘Boolese Pythagoreïsche Drietallenprobleem’ opgelost. Wie het bewijs wil controleren, zal zich door een bestand van 200 terabyte heen moeten ploegen, een record. Of je gelooft de computer op zijn woord: de getallen 1 tot 7824 voldoen wel aan de wiskundige regel van dit probleem, de getallen vanaf 7825 en hoger niet. Met deze prestatie won het team een prijs van honderd dollar.

3 juni 2016

Ruim tweeduizend jaar lang is een wiskundig bewijs typisch mensenwerk geweest. Het is een onweerlegbare opeenvolging van logische stappen, die in principe voor ieder mens te begrijpen moet zijn. Toch zijn wiskundigen de laatste decennia, met tegenzin, gewend geraakt aan bewijzen die worden geschraagd door onmenselijk lange computerberekeningen. Een pionier in dat opzicht was het bewijs voor het Vierkleurenprobleem

Samen met wetenschapsjournalist Kathryn Bowers, schreef Barbara Natterson het boek ‘Dierenbrein en mensenlijf’. — Het bewijs is 200 terabyte groot, overeenkomend met honderd miljoen dikke boeken (als pdf). Als je al die boeken samenvoegt tot één boek, zou het ongeveer deze omvang hebben, een boek waar je een wandeling op kan maken.
The House of Books

Maar het kan nog gekker: een computer heeft nu een bewijs geleverd, dat niet alleen langer is dan de mens ooit kan controleren, het is zelfs te groot om te printen of te downloaden, zodat anderen het niet rechtstreeks kunnen bekijken. De berekening die Marijn Heule, Oliver Kullmann en Victor Marek van de universiteit van Texas lieten uitvoeren op de Stampede-supercomputer leverde een bestand op van 200 terabyte, qua omvang vergelijkbaar met de gezamenlijke collectie boeken van alle Nederlandse bibliotheken.

Samenvatting van slechts 68 gigabyte

Gelukkig hoeven andere wiskundigen niet af te reizen naar Texas als ze het bewijs willen inzien. Heule en zijn collega’s hebben namelijk een soort gereedschapskist met gebruiksaanwijzing gemaakt van ‘slechts’ 68 gigabyte, waarmee het volledige bewijs op een andere supercomputer te reproduceren is.

Het bewijs lost het _Boolese (spreek uit: Boelse, naar George Boole) Pythagoreïsche Drietallen_-probleem op. Pythagoreïsche drietallen zijn setjes gehele getallen die de lengtes van de zijden van een rechthoekige driehoek kunnen vormen. Vanwege de stelling van Pythagoras, a² + b² = c², kun je nagaan dat bijvoorbeeld (3,4,5), (6,8,10), (5,12,13) en (9,12,15) pythagoreïsche drietallen zijn (want 3² + 4² = 5², enzovoort). Dit zijn meteen alle pythagoreïsche drietallen met zijden van maximaal 15.

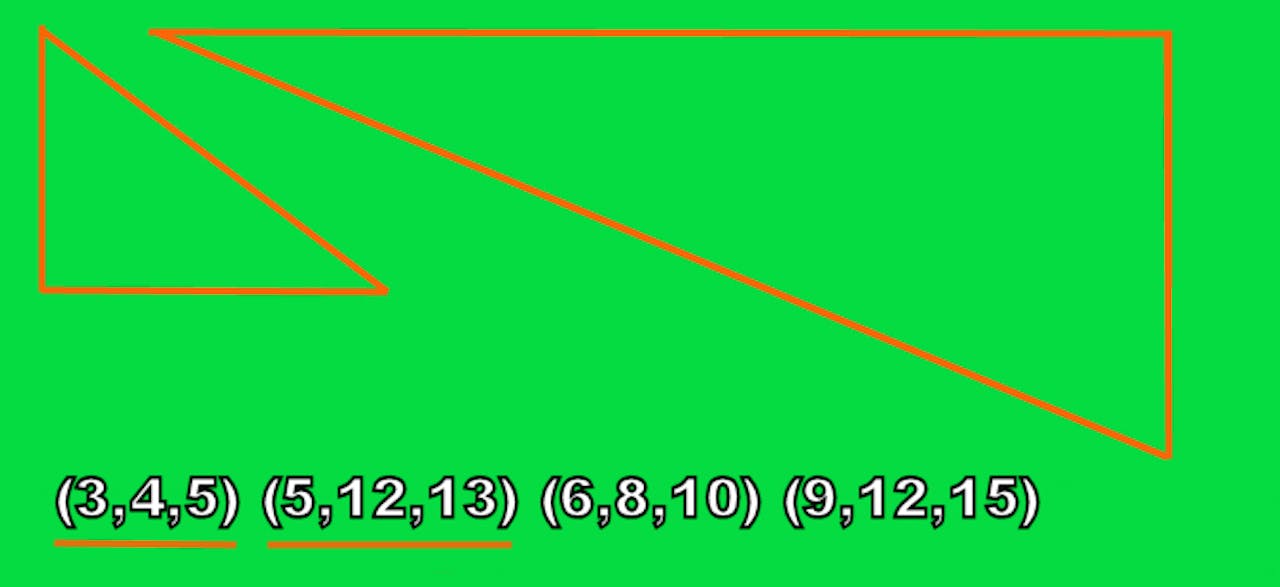
De pythagoreïsche drietallen met zijden tot en met 15. De rechthoekige driehoeken van de twee rood onderstreepte drietallen zijn getekend.
aj

Tweedelingen natrekken

De vraag die je nu kunt stellen is: kun je de getallen 1 tot en met 15 in twee setjes verdelen, zodanig dat in geen van beide sets een pythagoreïsch drietal zit? Dat kan. Een voorbeeld is:
I: [3, 6, 9, 13] en II: [ 1, 2, 4, 5, 7, 8, 10, 11, 12, 14, 15]

In dit speciale geval, N = 15, is simpel in te zien dat de tweedeling aan de eis voldoet. Want elk van de vier pythagoreïsche drietallen bevat minstens één getal dat uniek is voor dit drietal. Dus als je een uniek getal uit elk van de drietallen in I stopt, en de rest in II, kan I noch II een pythagoreïsch drietal bevatten.
Als je dit niet weet, zou je voor zowel I als II moeten controleren of er pythagoreïsche drietallen in voorkomen. Met I ben je snel klaar. Er zijn maar vier mogelijkheden: (3,6,9), (3,6,13), (3,9,13), (6,9,13) en die zijn niet pythagoreïsch. Maar in II heb je al 165 mogelijke drietallen, die je allemaal moet controleren. Pas dan weet je, of je tweedeling aan de eis voldoet.

Als je de grens hoger legt dan N = 15, bij N = 100 of N = 1000, zijn er veel meer pythagoreïsche drietallen, en de simpele redenatie over unieke getallen hierboven gaat dan niet meer op. Dan moet je alle 2^N tweedelingen uitproberen en elke keer alle mogelijke drietallen controleren. Dat zijn astronomische aantallen.

N_max

Voor kleine N was allang vastgesteld, dat er tweedelingen bestaan die aan de eis voldoen. Maar het is wel duidelijk, dat het steeds moeilijker wordt om zo’n tweedeling te vinden naarmate N groter wordt. Het Boolese Pythagoreïsche Drietallenprobleem stelt de vraag, of er een grootste N_max bestaat waarvoor zo’n tweedeling bestaat, terwijl die voor alle grotere N niet bestaat.

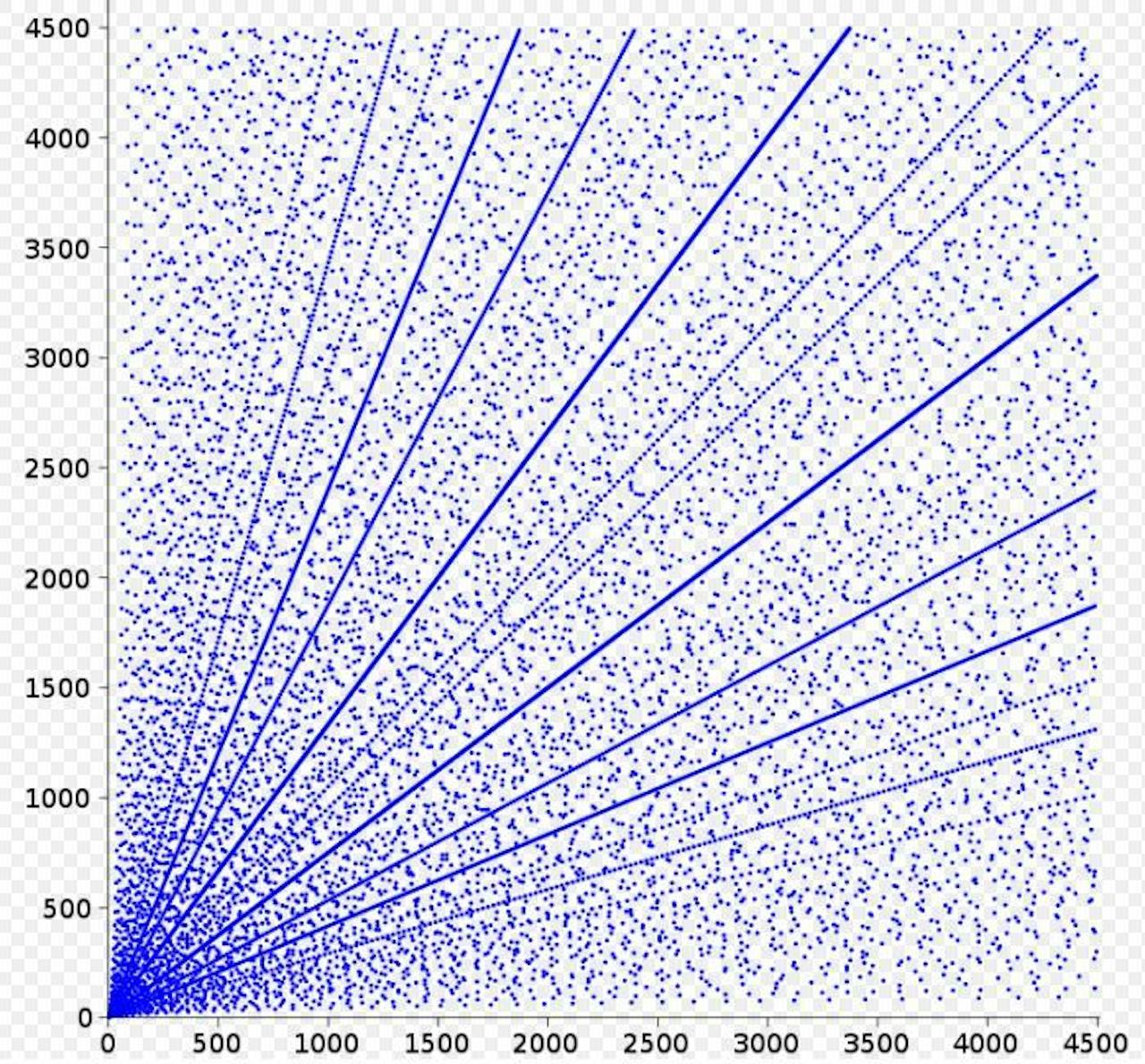
Diagram van alle pythagoreïsche drietallen tot 4500. Elk punt met coördinaten (a,b) stelt een drietal (a,b,c) voor. Het getal c voldoet aan c²=a²+b², die waarde is niet zichtbaar. Lijnen in het diagram zijn in werkelijkheid dicht opeen liggende losse punten.
Wikipedia

Het antwoord is: inderdaad, die N_max bestaat. Voor N = 1,2,3,……, 7824 kun je tweedelingen zonder pythagoreïsche drietallen vinden, voor N = 7825 en alle grotere N lukt dat niet. Eerder was, met gewone wiskunde, een ondergrens voor N_max gevonden van ongeveer 7600, en de computer is van daar af verder gaan zoeken.

Inlijsten

Met dit bewijs, waar een van de grootste supercomputers ter wereld twee dagen en nachten lang op heeft staan number crunchen, sleepte het team een prijs van honderd dollar (!) in de wacht, die twintig jaar geleden is uitgeloofd door wiskundige Robert Graham. Het uitloven van kleine geldprijzen voor dergelijke problemen is een traditie die is gestart door de befaamde Hongaar Paul Erdös, in een tijd dat wiskundigen nog uitsluitend met potlood en papier werkten. Overigens was het ook traditie om deze door Erdös uitgeschreven cheques niet te cashen, maar in te lijsten en aan de muur te hangen.

Het computerbewijs is in essentie een check van alle 2⁷⁸²⁵ mogelijke tweedelingen van de set 1,2,3,…….7825, waaruit blijkt dat ze allemaal minstens één pythagoreïsch drietal bevatten. Dat betekent ook, dat alle nog grotere tweedelingen eveneens pythagoreïsche drietallen bevatten.

2⁷⁸²⁵ is ongeveer 10²³⁵⁵, een 1 met 2355 nullen. Dit is zo’n gigantisch aantal, dat het ook voor de Stampede supercomputer onbegonnen werk was geweest om ze letterlijk een voor een na te kijken. Er is echter slim gebruik gemaakt van allerlei symmetrieën, waardoor je grote aantallen tweedelingen samen kunt nemen. Ook is deze enorme rekenklus goed te parallelliseren: je kunt er meerdere processors (chips) gelijktijdig aan laten rekenen, omdat ze niet afhankelijk zijn van elkaars resultaten. Stampede gebruikte voor deze klus achthonderd parallelle processors.

De helft van het bewijs

Als het pas voor N = 7825 niet lukt, moet het voor alle kleinere N wel lukken. Inderdaad vond Stampede voor N = 7824 een tweedeling zonder pythagoreïsche drietallen. Er zijn zelfs heel veel mogelijkheden.

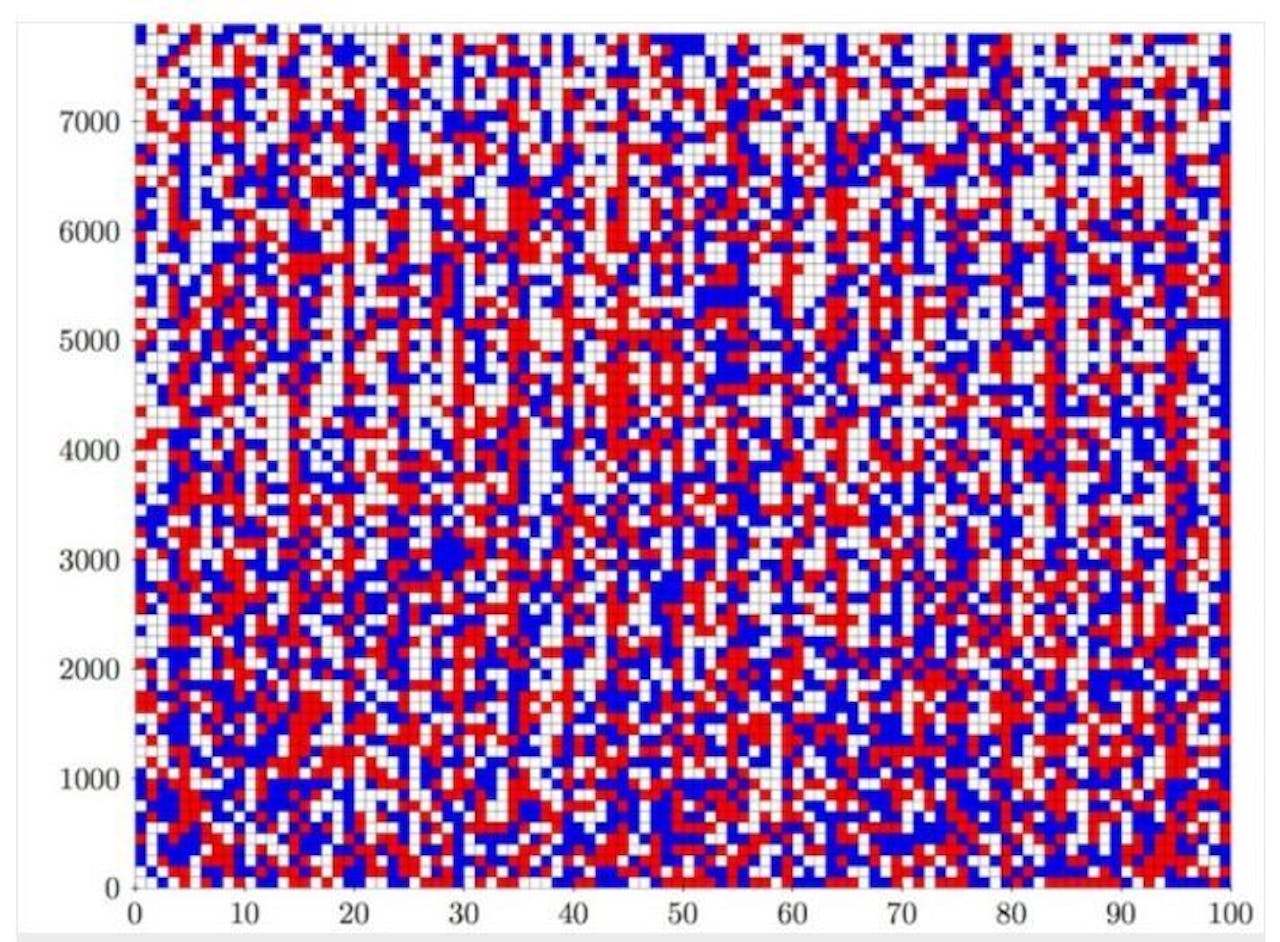
N_max=7824: de grootst mogelijke tweedeling van de getallen 1,2,3,…..die geen pythagoreïsche drietallen bevat. De blauwe getallen zitten in deel I, de rode in deel II. De witte getallen mogen zowel in I als in II gezet worden.
Marijn Heule

Eigenlijk is dit nog maar de helft van het bewijs. Al bij de eerste computerbewijzen merkten kritische wiskundigen op, dat deze methode het probleem alleen maar verschuift. Immers, de uitkomst wordt geproduceerd door ingewikkelde software, die uit duizenden regels code kan bestaan. Hoe bewijs je dat er geen fout in die software zit?

Zelfs daar bestaat tegenwoordig software voor. Deze rafelt het computerprogramma uiteen in een groot aantal elementaire stappen die bewezen correct zijn. Ook is zo te checken, dat het programma doet wat het zegt te doen. Natuurlijk kun je je ook afvragen of deze software-checker wel correct is. Maar deze is uit en te na getest en al op allerlei andere software toegepast, zodat de kans dat die niet correct is te verwaarlozen valt. Echter, een software-checker is erg omslachtig en produceert enorm lange correctheidsbewijzen. Het bestand van 200 terabyte is in feite het correctheidsbewijs voor het bewijs dat N_max = 7824.

Onbeslisbaar

Aan het slot van hun verslag, gepubliceerd op wetenschapssite ArXiv, stippen de onderzoekers een meer filosofische kwestie aan: is dit wel echte wiskunde? Leidt het wel tot dieper inzicht? Als er een ‘menselijk’ bewijs was gevonden voor dit specifieke probleem, dan kun je vaak vrij simpel ook een bewijs vinden voor een meer algemeen probleem, bijvoorbeeld, tot welke N_max er driedelingen zonder pythagoreïsche drietallen bestaan, vierdelingen, algemeen: k-delingen.

Dit computerbewijs voor tweedelingen komt neer op alle mogelijkheden checken. Het aantal mogelijkheden bij driedelingen is nog veel groter, dus dat bewijs zal waarschijnlijk nog groter zijn dan 200 terabyte. Het zou kunnen, dat de grootte van het bewijs voor k-delingen zo snel groeit met toenemende k, dat het algemene probleem volgens de axioma’s (‘spelregels’) van de gewone wiskunde noch waar is, noch onwaar, maar onbeslisbaar. Maar met deze computermethode zul je daar nooit achter komen.

Reageer