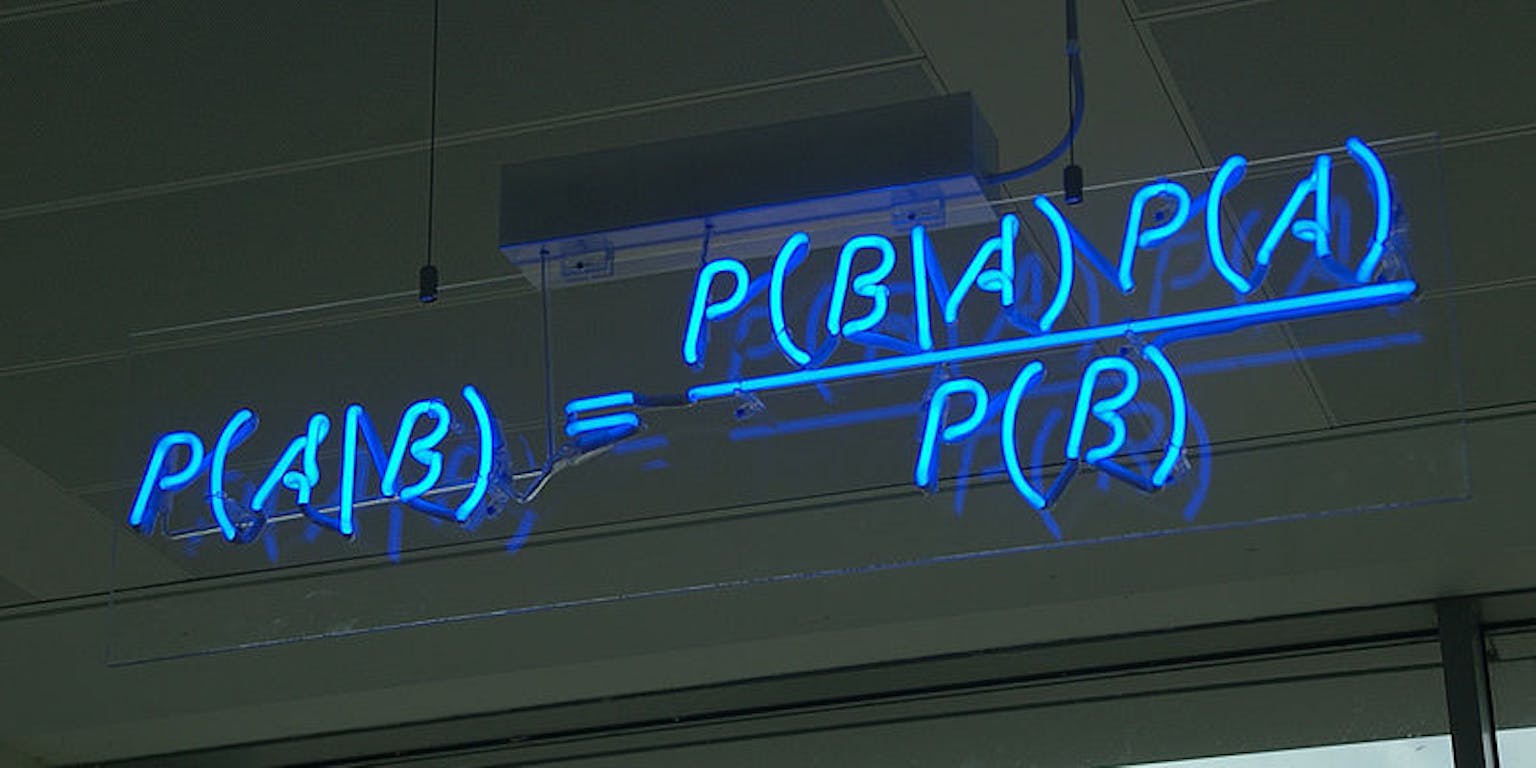De stelling van Bayes: nuttig of gevaarlijk?

De stelling van Bayes, die aan de bron ligt van een hele tak van statistiek, werd een week geleden in Science uitvoerig besproken door een statisticus van de Stanford-universiteit. Wat houdt de stelling in, en waarom is Bayesiaanse statistiek zowel nuttig als omstreden?

21 juni 2013

Thomas Bayes was een Britse statisticus in de achttiende eeuw. Hij had een revolutionair idee: wat als we kennis uit het verleden toe kunnen passen om statistische voorspellingen te maken? Op die manier zou je eerlijker voorspellingen krijgen, die bovendien niet blind zijn voor de wereld naast de statistiek, zoals de gewone, of frequentistische statistiek dat wel is.

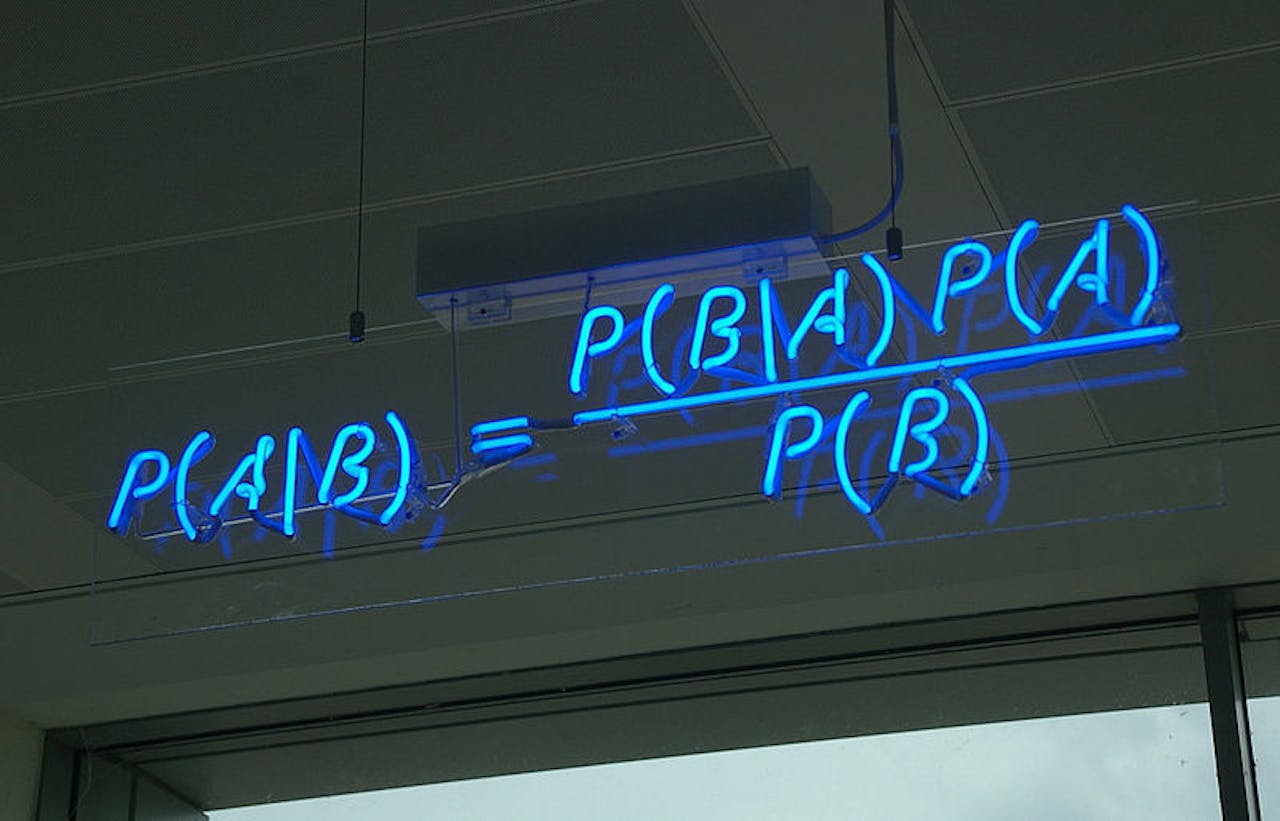
Een neonbord met daarop de P(A\B) formule weergegeven. — De stelling van Bayes in neonlicht
mattbuck, Wikimedia Commons

Tweelingen

Een mooi voorbeeld van Bayes theorem heeft te maken met tweelingen. Stel, een moeder weet dat ze zwanger is van een tweeling. Wat is dan de kans dat de tweeling een-eiig is? Doktors weten dat de kans op een een-eiige tweeling kleiner is dan op een ‘normale’ tweeling;. Maar op de echo ziet de arts dat de moeder twee meisjes in de buik heeft. Dat maakt de kans dat de tweeling eeneiig is groter.

Hoe bereken je dit nu? Daarvoor bestaat de stelling van Bayes. Deze zegt namelijk dat de kans dat de tweeling een-eiig is, gegeven dat de echo laat zien dat het twee meisjes zijn, hetzelfde is als de omgekeerde kans (de echo laat twee meisjes zien, gegeven dat de tweeling een-eiig is) keer de kans dat de tweeling identiek is gedeeld door de kans dat de echo twee meisjes laat zien (zie kader voor de precieze berekening).

Oktopus Orakel Paul ligt in het water. Er is ook een schoen afgebeeld. — De octopus in zijn aquarium. Inmiddels is hij helaas overleden.
Tilla, Wikimedia Commons

Een ander mooi voorbeeld waarin de Bayesiaanse methode beter werkt dan normale statistiek: octopus Paul. Deze Duitse octopus werd beroemd tijdens het WK voetbal van 2010, omdat hij de uitslag van een aantal wedstrijden achter elkaar goed voorspelde. Was Paul een helderziende ongewervelde? Een gewone statisticus zou het bijna moeten toegeven; hij had het zo vaak achter elkaar goed, dat de kans dat het toeval was wel érg klein werd.

Maar, zo legde wiskundige David Spiegelhalter uit, met Bayesiaanse statistiek prik je hier zo doorheen. Als je namelijk een conservatieve schatting maakt en zegt dat de kans op helderziendheid heel klein is, dan is de kans dat Paul helderziend is automatisch ook heel klein – ondanks al zijn correcte ‘voorspellingen’.

De kans op identieke kinderen berekenen

Hoe bereken je de kans op een meisjestweeling met Bayes? Laten we eerst de formule opschrijven:
P(A|B) = P(B|A)*(P(A)/B(B))
Waarbij in dit geval A het geval is dat er een identieke tweeling wordt geboren. B is de situatie dat de echo twee meisjes laat zien.

Dankzij Bayes hebben we voorkennis over de situatie: de kans op een een-eiige tweeling, P(A) is 1/3. De voorwaardelijke kans P(B|A) dat de kinderen twee meisjes zijn als er een een-eiige tweeling geboren wordt is 1/2, de kans op jongens is immers even groot als de kans op meisjes. De kans dat de echo twee meisjes laat zien, P(B), is iets ingewikkelder te berekenen. We moeten namelijk de kans dat het twee meisjes zijn, gegeven dat het een identieke tweeling is, los berekenen van de kans dat het twee meisjes zijn als het geen identieke tweeling is. Vervolgens moeten we deze twee kansen vermenigvuldigen met de kans dat ze gebeuren (1/3 kans op een identieke tweeling). Dat levert op dat P(B) = 1/2*1/3 + 1/4*2/3 = 1/3.

Nu hebben we alle onderdelen van de formule, en kunnen we dus P(A|B) uitrekenen: de kans dat de baby’s identiek zijn, gegeven dat de echo twee kinderen van hetzelfde geslacht laat zien. Deze kans is nu
P(A|B) = 1/2*((1/3)/(1/3)) = 1/2.
We zien dan dus dat de kans op ene identieke tweeling in dit geval precies even groot is als de kans op een normale tweeling.

Thomas Bayes

Gezien de invloed die Bayes heeft gehad op de statistiek, was hij eigenlijk een wetenschapper van niks. Hij publiceerde twee artikelen in zijn hele leven, waarvan eentje niet eens over wiskunde ging, maar over theologie. Zijn belangrijkste idee, de stelling van Bayes, publiceerde hij nooit zelf. Pas na zijn dood, toen een vriend van hem zijn werk uitbracht, kwam de stelling in de openbaarheid, waarna hij in de volgende eeuwen aan populariteit won.

Schimmige aannames

Bayes’ is nog steeds omstreden, omdat de voorgaande kennis vaak niet helemaal helder gedefnieerd is. Wat mag je wel meenemen in je berekening, en wat niet. De meeste wetenschappelijke onderzoeken maken gebruik van statistiek, om aan te tonen dat de resultaten niet op toeval berusten. Maar dat is bijna altijd de frequentistische statistiek, omdat die geen aannames maakt en daardoor neutraal is. Maar, zeggen de aanhangers van Bayes, dat is onzin. Vaak is juist het negeren van de wereld om een onderzoek heen een oorzaak van verkeerde onderzoeksresultaten.

Bradley Efron, die het Science-artikel schreef, is een tijdlang redacteur geweest bij een vaktijdschrift voor statistiek. Hij zag daar maar weinig Bayesiaanse statistiek langskomen. Dat betekent volgens hem echter zeker niet dat Bayes afgeschreven moet worden. Integendeel: nu de wetenschap steeds ingewikkelder wordt is juist de Bayes-methode krachtig. Daarmee kan je namelijk eerdere wetenschappelijke kennis verweven in je onderzoek, om daarmee een overtuigender statistiek te maken.

De risico’s van Bayes bestaan echter nog steeds. Verkeerde aannames of teveel informatie in je statistiek gebruiken kan voor vertekende en oneerlijke resultaten leiden. Het is dan ook belangrijk om ook met Bayes eerlijk en redelijk te blijven. Die grens is dun, geeft Efron toe, maar het kan wel.

Hij sluit af door te zeggen dat hij de ruzie tussen Bayes-wiskundigen en de normale statistici niet gaan oplossen. De argumenten voor en tegen zijn beiden overtuigend. Bovendien, de twee vormen van rekenen bestaan al 250 jaar naast elkaar – waarom zou het niet gewoon zo verder kunnen gaan?

Bron