Origami: de oeroude kunst om van een vel papier, zonder scheuren of plakken, een driedimensionaal object te vouwen. Pas nu is een methode gevonden om systematisch nieuwe origamipatronen te ontwerpen die opvouwen zonder te wringen.
Zitten natuurkundigen op het Huygens Laboratorium in Leiden en het AMOLF in Amsterdam, echt van onze belastingcenten te spelen met vouwblaadjes? Inderdaad. Origamipatronen zijn al jaren een serieus onderwerp van onderzoek, en in sommige fases komt er nog schaar, plakband en papier aan te pas.
Origami is relevant als je een gecompliceerde 3D-vorm efficiënt wilt opvouwen, en weer automatisch laten uitvouwen. Bijvoorbeeld grote zonnepanelen, of een robot met acht ledematen die in een overvolle, onbemande ruimtecapsule gelanceerd wordt. Ikea-meubels die zichzelf in elkaar zetten zouden trouwens ook wel handig zijn.

Een origamipatroon dat tot twee heel verschillende 3D-vormen kan worden opgevouwen. Alle door Martin van Hecke en zijn collega’s ontdekte origamipatronen kunnen op twee of meer manieren worden opgevouwen.
Martin van Hecke e.a., Nature PhysicsTot nu toe was er echter geen systematische methode om nieuwe vouwpatronen te ontdekken, of hun eigenschappen te voorspellen. Als je willekeurig wat vouwen maakt in een vel papier, zal de zaak meestal al snel vastlopen: de ene vouw zit de andere in de weg. Met papier kan je dan nog wat smokkelen door het in een bocht te vouwen, maar dat ‘mag’ niet. Een geldig vouwpatroon is star: je kun het zelfs maken uit stijve panelen die door scharnieren met elkaar verbonden zijn.

De Mars-vouwing, een origamipatroon ontwikkeld door NASA om een opvouwbare warmteradiator te maken.
Brigham Young UniversityKnooppunten van vouwen
Natuurkundige Martin van Hecke en drie collega’s hebben nu wel zo’n methode voor starre vouwingen ontwikkeld. Hoe kom je op zoiets? Van Hecke: “We hebben heel lang zitten broeden op twee al lang bekende origamipatronen, het Huffman-patroon en het Mars-patroon: waarom vouwt dat?”
Ze realiseerden zich dat de relevante bouwstenen van een vouwing niet de vouwen zelf zijn, maar de knooppunten van vouwen, punten waar vier of meer vouwlijnen bij elkaar komen (als er maar drie bij elkaar komen, vouwt het papier sowieso niet).
Zo’n knooppunt wordt volledig bepaald door de vier hoeken tussen de lijnen die in het knooppunt samenkomen – uiteraard moet de som van die hoeken 360 graden zijn. Zonder verdere randvoorwaarden zijn oneindig veel knooppunten mogelijk, maar Hecke en zijn team ontdekten vier speciale knooppunten die bijzonder geschikt zijn om geldige vouwingen mee te maken.
Als in alle knooppunten vier vouwen samenkomen, bestaat het vouwpatroon uit louter vierhoekige (over het algemeen scheve) tegels. Omdat je op elk van de vier hoeken een van die vier knooppunten kunt neerzetten in één van vier mogelijke oriëntaties, zijn in totaal 164 = 65.536 tegels mogelijk.
140 tegels
Dat zijn er heel wat, maar dat was nog wel een behapbaar aantal, omdat een geldige vouwing nog twee wiskundige randvoorwaarden oplegt aan welke combinaties van hoekpunten toelaatbaar zijn. Daardoor bleven nog maar 140 tegels over waar je starre vouwingen mee kunt maken. Van Hecke: “We vermoeden dat we ze allemaal gevonden hebben, maar dat hebben we niet bewezen. Dat laten we graag aan de wiskundigen over.”
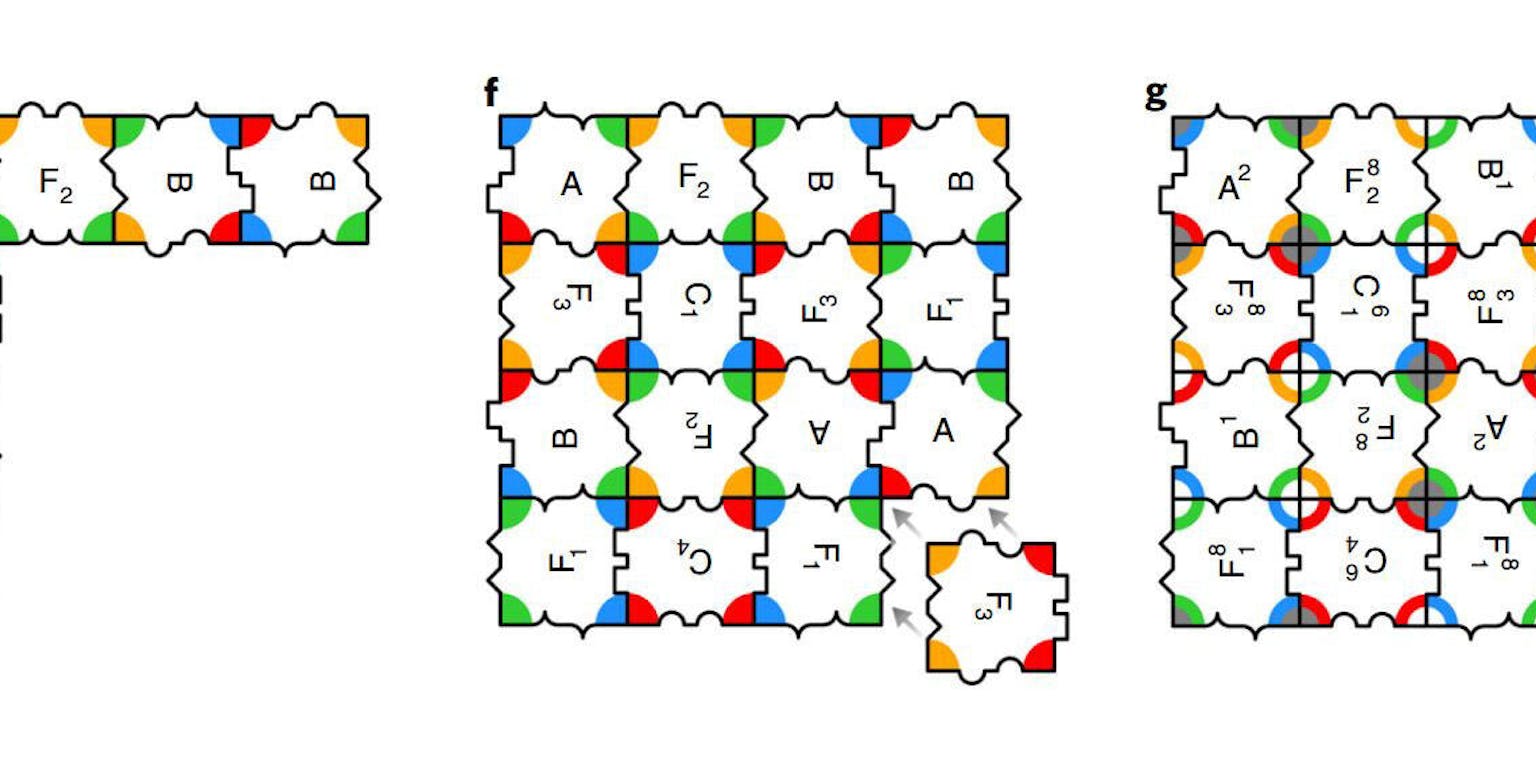
Het mooie is, dat je van die 140 tegels, met een paar extra spelregels, in allerlei combinaties tegelvloertjes kunt leggen die ook vouwbaar zijn. Symbolisch worden die scheve tegels voorgesteld door vierkante puzzelstukjes met uitsteeksels die bepalen in welke combinaties je de 140 tegels aan elkaar mag leggen (zie illustratie bovenaan dit artikel). Zo is ineens een astronomisch aantal starre vouwpatronen toegevoegd aan de weinige die tot nu toe bekend waren.
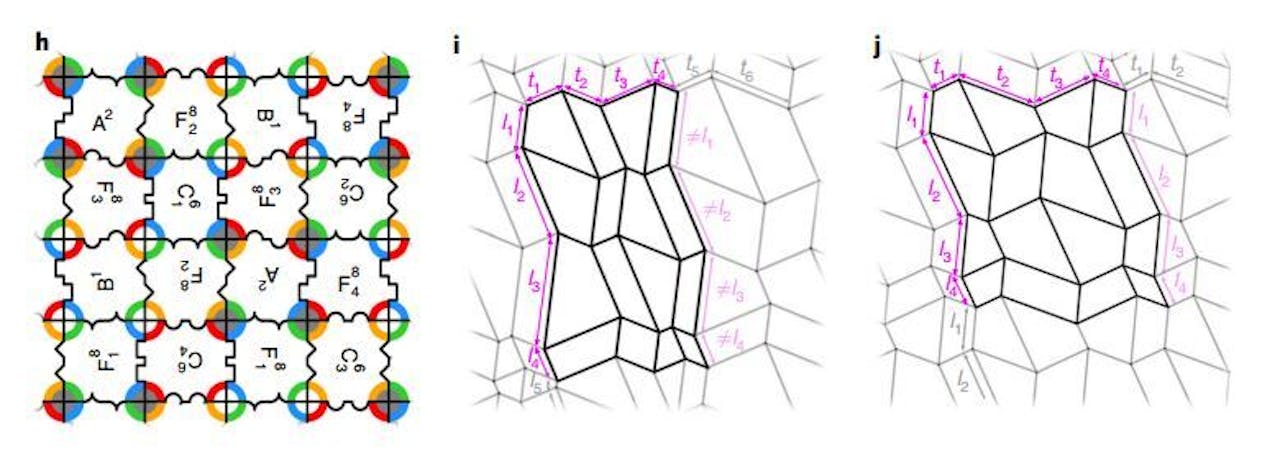
De onderzoekers ontdekten een set van 140 basistegels, waarmee je volgens bepaalde regels patronen kunt leggen. Elk tegelpatroon (links) correspondeert met een vouwpatroon, maar de lengte van sommige zijden kan nog variëren. Daardoor ontstaan verschillende varianten van het vouwpatroon, die zowel periodiek (rechts) als niet-periodiek (midden) kunnen zijn.
Martin van Hecke e.a., Nature PhysicsAlfa of omega
Volgens Van Hecke wijken ze ook af van de regelmatige vouwpatronen die tot nu toe bekend waren: “Heel veel van die vouwingen zien er schots en scheef uit, en ze vouwen ook altijd op meer dan één manier.”
Dat laatste kan interessant zijn voor ontwerpers van metamaterialen. Een metamateriaal kan bestaan uit twee verschillende materialen die verschillend reageren op, bijvoorbeeld, elektrische spanning die je erop zet. Een star vouwpatroon van zo’n metamateriaal zou dan twee compleet verschillende ruimtelijke vormen aan kunnen nemen, afhankelijk van het feit of de spanning ‘aan’ of ‘uit’ staat. De onderzoekers hebben als voorbeeld in een plastic plaat een vouwing gemaakt die naar keuze de vorm van de Griekse letter alfa of omega aanneemt – al moet je deze nog wel met de hand ombouwen.
Het in kaart brengen van alle mogelijke starre vouwingen is in wezen een puur wiskundig probleem, dat nog lang niet volledig is opgelost. Maar voor toekomstige praktische toepassingen is de gereedschapskist nu alvast goed gevuld.