Naar de content

Alleen ter plekke ontcijferbaar

Amsterdamse quantumcryptografen werken aan een geheimschrift dat maar op één plaats op aarde leesbaar is.

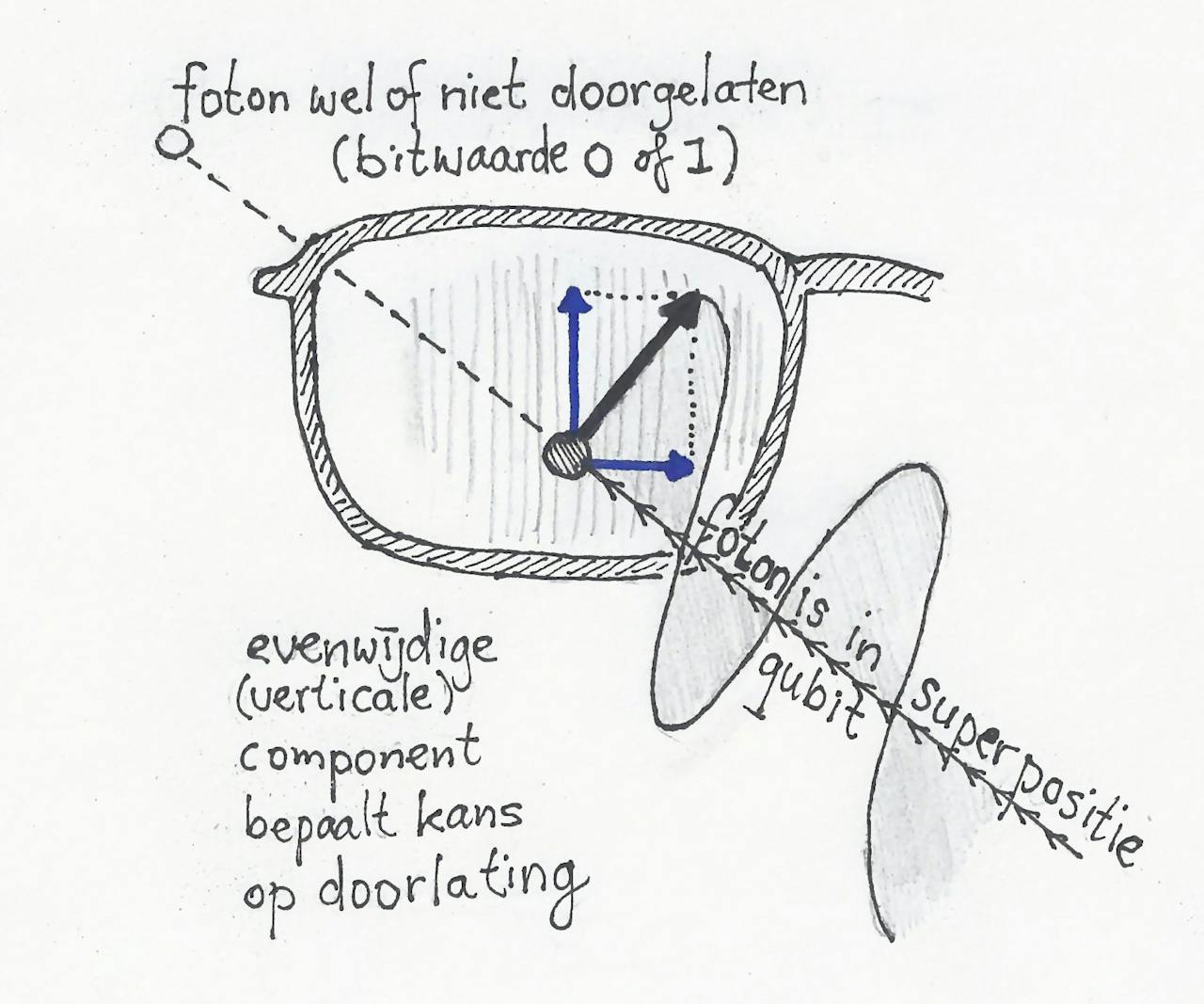
Onkraakbare geheimschriften bestaan al, maar voor echt veilige communicatie is méér nodig. Je wilt ook zeker weten dat de afzender geen bedrieger is. Zo weet je dat je geheim agent niet gekidnapt is, of dat je echt met de regering van Zuid-Korea praat, niet die van Noord-Korea. Absoluut veilig kan niet, maar het verschil is te verwaarlozen.

17 april 2015

Tegenwoordig loopt bijna iedereen met een apparaat rond dat je locatie verraadt, namelijk je smartphone. Die zendt telkens signalen naar de dichtstbijzijnde vaste zendmasten, ook als je niets met je telefoon doet, zodat je door de sterkte van het signaal in die ontvangers met een foutmarge van enige tientallen tot honderden meters te localiseren bent. Tenzij je je telefoon kwijt bent of opzettelijk ergens hebt laten liggen, natuurlijk.

Plaatsgebonden cryptografie is veel ambitieuzer, die wil met praktisch honderd procent zekerheid vaststellen dat je gesprekspartner, bijvoorbeeld, zich bevindt in het Torentje van de minister-president. Plaatsgebonden cryptografie zal waarschijnlijk vooral toepassingen vinden bij communicatie die extreem veilig moet zijn, zoals tussen regeringsleiders, ambassades, legercommandanten en geheim agenten.

Lichtsnelheid

Het basisprincipe is simpel en komt uit Einsteins relativiteitstheorie: geen enkel signaal kan sneller gaan dan de lichtsnelheid. Dus jij – de Verifieerder- stuurt iemand een radiosignaal met een onvoorspelbare boodschap, bijvoorbeeld een willekeurige serie cijfers: ‘3411095467237207’. Die ander – de Identificeerder – stuurt precies dezelfde boodschap terug. Als dit antwoord na exact een duizendste seconde bij jou aankomt, dan kan de Identificeerder hoogstens de helft van 300 kilometer verderop zitten (eigenlijk de helft van 299 kilometer, 792 meter en 458 millimeter, want de lichtsnelheid is exact 299.792.458 meter per seconde). Dat bakent dus rondom jou zelf een cirkel met straal 150 kilometer op het aardoppervlak af.

Als jij een tweede Verifieerder op een vaste positie hebt die je vertrouwt, die ook een radiosignaal naar de Identificeerder stuurt, krijg je twee cirkels die elkaar deels overlappen. Met drie Verifieerders overlappen de drie cirkels in principe in één punt. Dat hangt wel af van hoe snel de Identificeerder reageert; als hij een microseconde wacht met zijn radiosignaal terugsturen, zit er al een speling van minstens driehonderd meter in de positiebepaling (want zo ver reist het licht in een microseconde).

Uiteraard hebben we het niet over handmatige communicatie, het zal gaan om signaaluitwisseling tussen elektronische systemen. Harry Buhrman: “Dit soort elektronica heeft een reactiesnelheid van ongeveer een nanoseconde, wat inhoudt dat je tot op dertig centimeter nauwkeurig te localiseren bent.”

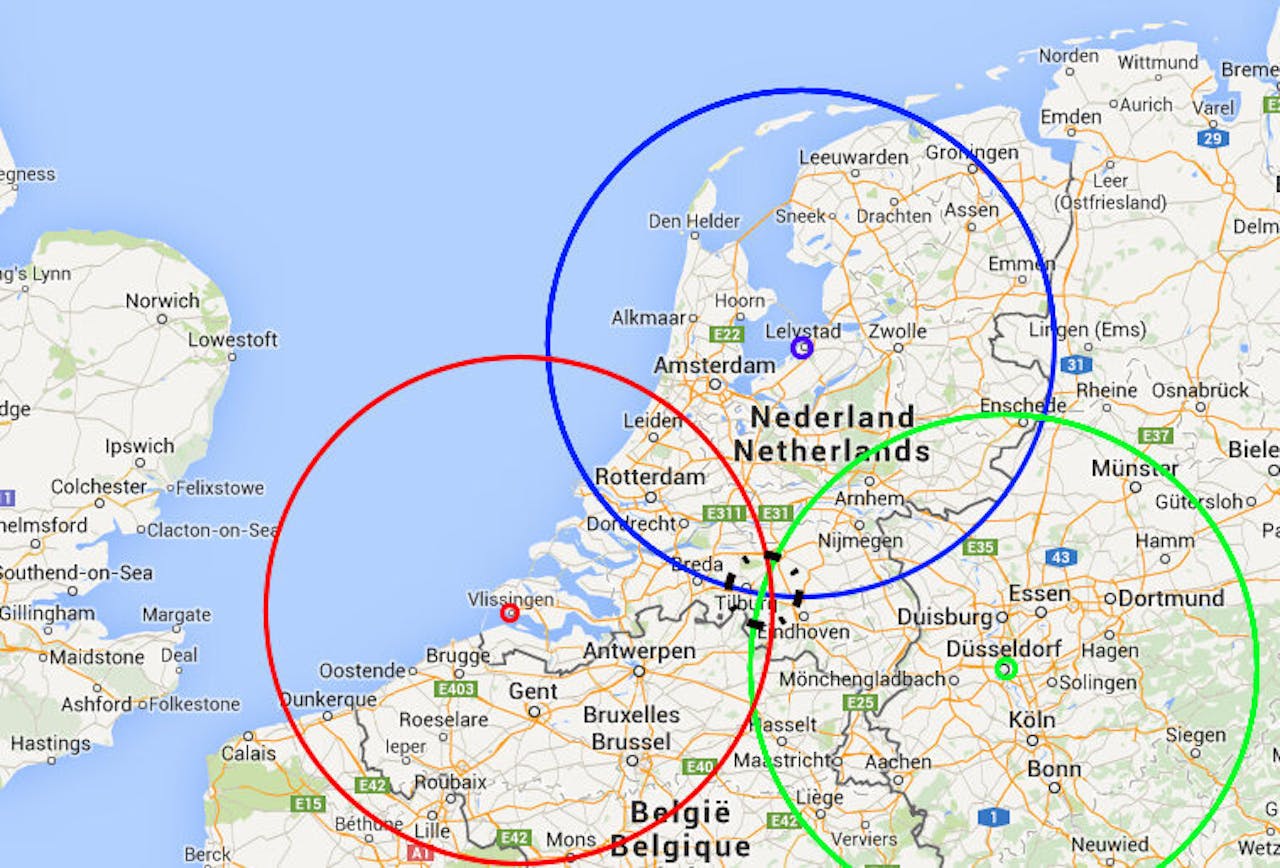
Drie Verifieerders in Lelystad, Vlissingen en Düsseldorf zenden een oproepsignaal uit. Zodra er antwoord komt van de Identificeerder, kunnen ze uit de tijd tussen het verzenden en de binnenkomst van het antwoord elk de maximale afstand tot de Identificeerder bepalen, die zich in dit geval bij Tilburg bevindt, de plek waar de drie cirkels overlappen.

 AJ

Duivels slimme slechterikken

Dit principe van ‘uitpeilen’ met radiosignalen is ook in grote lijnen hoe GPS werkt. Maar cryptografen leven in een denkwereld waar je er altijd vanuit gaat dat duivels slimme slechteriken proberen je te bedriegen. Stel dat je in veilig contact probeert te treden met iemand waarvan je hoopt dat hij in een andere stad 150 kilometer verderop zit. Als nu een Bedrieger, die vlak bij jou in de stad zit, jouw boodschap ‘3411095467237207’ opvangt en precies lang genoeg wacht alvorens deze boodschap terug te sturen, kan hij je doen geloven dat deze al die tijd onderweg is geweest, en dus van 150 kilometer ver komt. Om meerdere Verifieerders te misleiden zijn in het algemeen meerdere Bedriegers op diverse locaties nodig, maar zoals gezegd, cryptografen die proberen een veilig systeem te ontwerpen, gaan altijd uit van de ergste denkbare mogelijkheid.

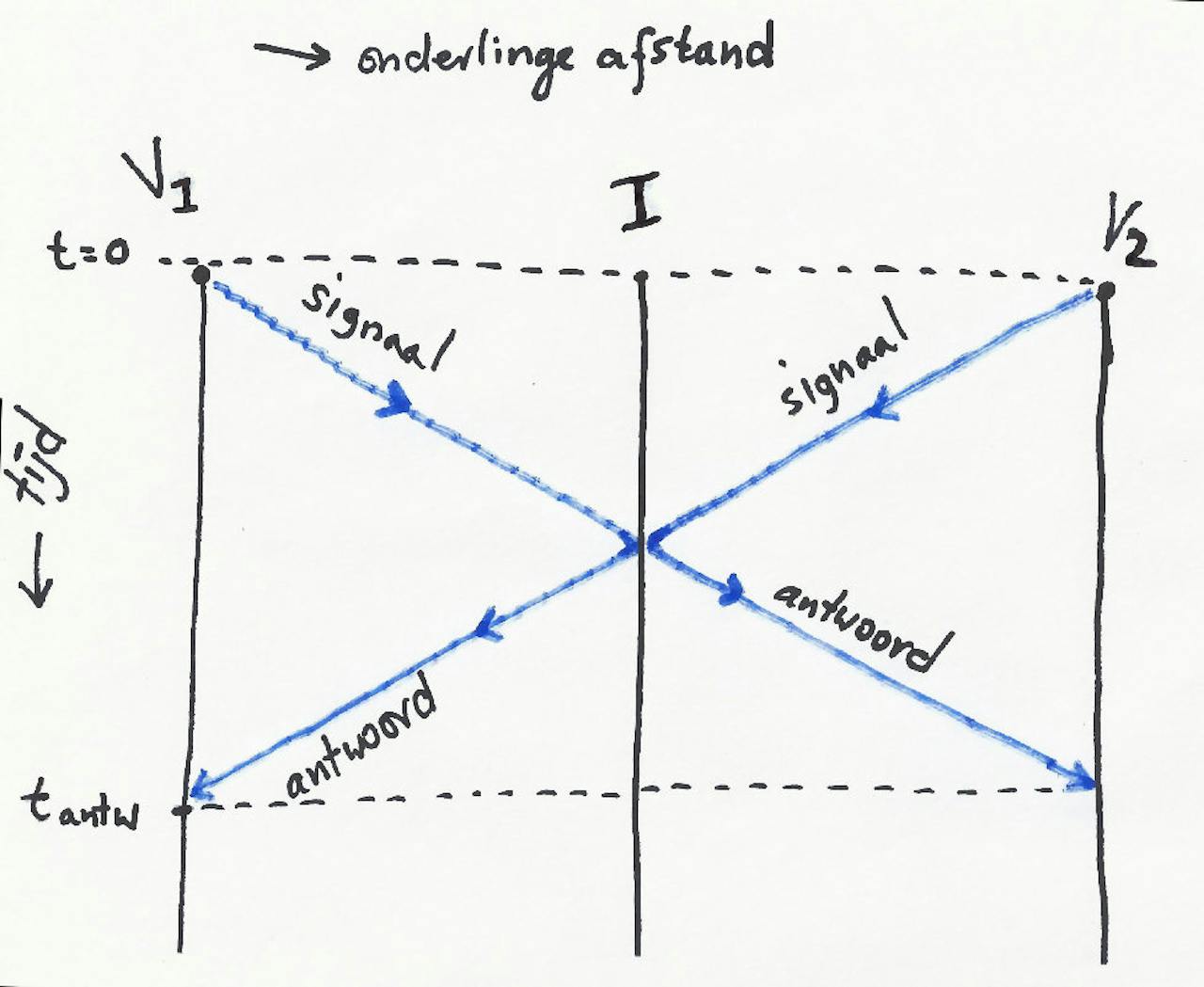
Klassiek seinen
Het verifiëren van iemands positie in een 1-dimensionale ruimte, dus als iedereen op één lijn zit. De tweede dimensie is de tijd, die van boven naar beneden loopt. De twee Verifieerders V1 en V2 en de Identificeerder I blijven op hun plek, zodat hun wereldlijnen recht naar beneden lopen. Ze sturen elkaar licht- of radiosignalen. Geen enkel signaal kan sneller dan het licht, dus een blauwe lijn kan nooit horizontaler lopen dan deze.

 aj

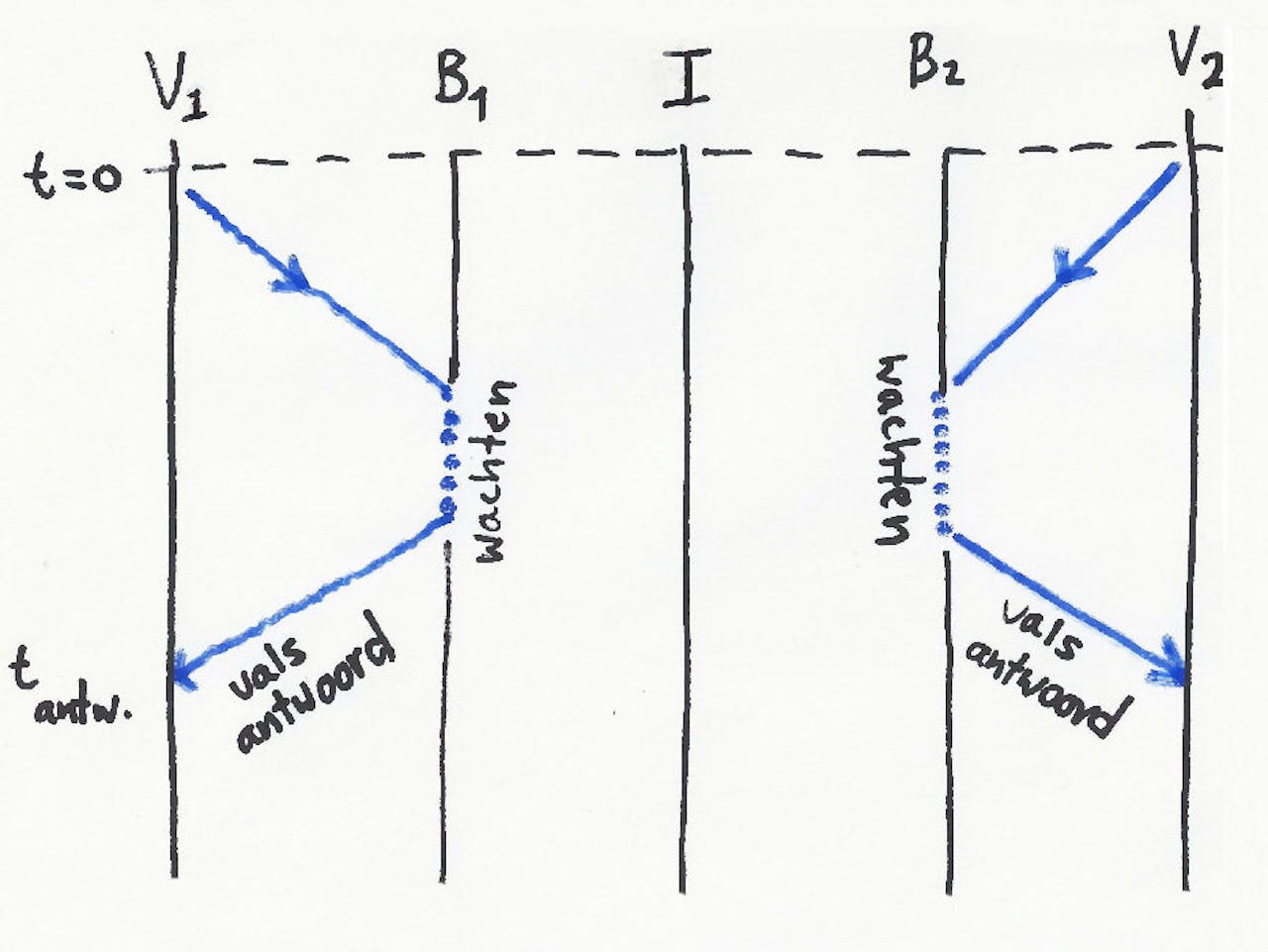
Klassiek bedriegen
Maar: twee Bedriegers kunnen altijd de signalen onderscheppen en de Verifieerders doen geloven dat de antwoorden afkomstig zijn van de Identificeerder. In meer dimensies zijn meer Bedriegers nodig, maar het lukt altijd.

 aj

Sinds 2009 weten cryptografen dat plaatsgebonden cryptografie niet mogelijk is wanneer je alleen maar klassieke radiosignalen of laserbundels (of postduiven) naar elkaar stuurt. Vier cryptografen, Nishanth Chandran, Vipul Goyal, Ryan Moriarty en Rafail Ostrovsky, bewezen toen dat elk denkbaar protocol waarbij de Verifieerders en een Identificeerder elkaar klassieke boodschappen sturen, gehackt kan worden. Bedriegers zijn dus altijd in staat om de Verifieerders om de tuin te leiden en ze te laten geloven dat zij op de plaats van de Identificeerder zitten.

Qubits en EPR-paren

Zonder de wonderen van de quantumwereld zou het in 2009 dus einde verhaal geweest zijn voor de plaatsgebonden cryptografie. Maar inmiddels hadden fysici al leren werken met qubits en EPR-deeltjesparen: niet-klassieke, mysterieuze quantumobjecten die zich in zekere zin niet houden aan Einsteins maximumsnelheid. Weliswaar kun je ook met EPR-paren geen informatie sneller dan het licht overseinen, maar je kunt er wel correlaties tussen twee verafgelegen gebeurtenissen mee teweegbrengen. Zou met deze quantumboodschappers plaatsgebonden cryptografie toch mogelijk zijn?

Om te begrijpen hoe dit werkt, gaan we de situatie drastisch vereenvoudigen, tot één dimensie. De Identificeerder (I) bevindt zich ergens op een rechte lijn, met aan de uiteinden twee Verifieerders (V1 en V2), die willen vaststellen of de Identificeerder tussen hen in zit. Maar aan beide kanten zit ook nog een Bedrieger op de lijn, links B1 en rechts B2. De klassieke stand van zaken zie je in de twee diagrammen hierboven. Maar als je een qubit kunt versturen, is de situatie wezenlijk anders.

V1 stuurt een qubit naar I, en V2 stuurt de keuze van de meting die I aan het qubit moet doen (deze keuze hebben V1 en V2 van tevoren afgesproken). I moet de uitkomst meteen terugsturen aan allebei, maar die klopt alleen als hij zowel het qubit als de keuze voor de meting ontvangen heeft (zie het kader ‘Qubits meten’).

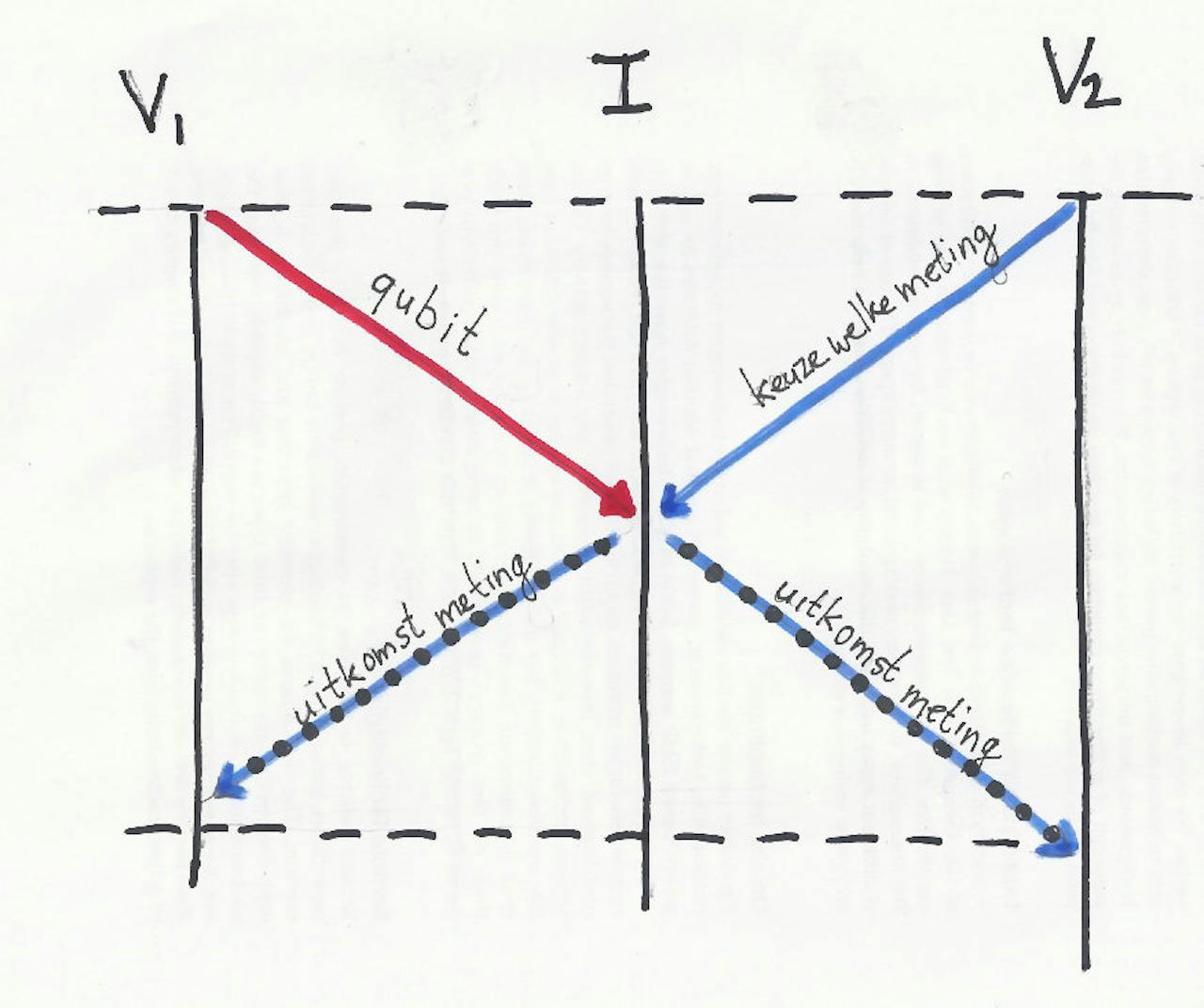
Seinen met qubits
Om de plaats van de Identificeerder vast te stellen, stuurt Verifieerder 1 hem een qubit toe, en Verifieerder 2 welke meting hij daarop moet uitvoeren. Alleen de combinatie van het qubit en deze meting levert de juiste uitkomst op. Rood is een quantumsignaal, blauw een klassiek signaal. De tijd loopt weer van boven naar beneden.

 aj

Dit zou ook nog met klassieke signalen kunnen, maar het voordeel van het qubit blijkt pas als er twee Bedriegers (B1 en B2) op de lijn zitten. Die proberen, net als in het diagram ‘Klassiek bedriegen’, de signalen te onderscheppen om te doen alsof zij op de plek van I zitten. Het blijkt nu een cruciaal verschil te maken, dat de signalen van V1 en V2 niet gelijktijdig bij B1, noch bij B2 aankomen.

Om op tijd de uitkomst van de juiste meting naar V1 te sturen, zou B1 het qubit van V1 moeten bewaren totdat hij bericht van B2 heeft, maar die qubit zou hij ook moeten doorsturen naar B2, zodat die zijn uitkomst van de meting op tijd naar V2 kan sturen. Met een gewone bit informatie is dat natuurlijk geen probleem: je kopieert gewoon de waarde van de bit (0 of 1) en stuurt die door. Maar een qubit is echt een heel ander ding, dat is een superpositie van de mogelijke uitkomsten 0 en 1. Een wet van de quantumtheorie (het ‘kloonverbod’) maakt het onmogelijk om een qubit te kopiëren. Als je dat toch probeert, dan is dat een meting van het qubit, waardoor de superpositie van 0 en 1 verloren gaat, je houdt als uitkomst een bit over met de waarde 0 of 1. Die bitwaarde kan B1 wel naar B2 sturen, maar daar heeft B2 niets aan, omdat hij daarmee niet de uitkomst kan berekenen, die hij zou hebben gekregen als hij een meting aan het qubit gedaan had. Als het je nu duizelt: neem even rustig de tijd om het diagram ‘Een qubit is niet te klonen’ te bekijken.

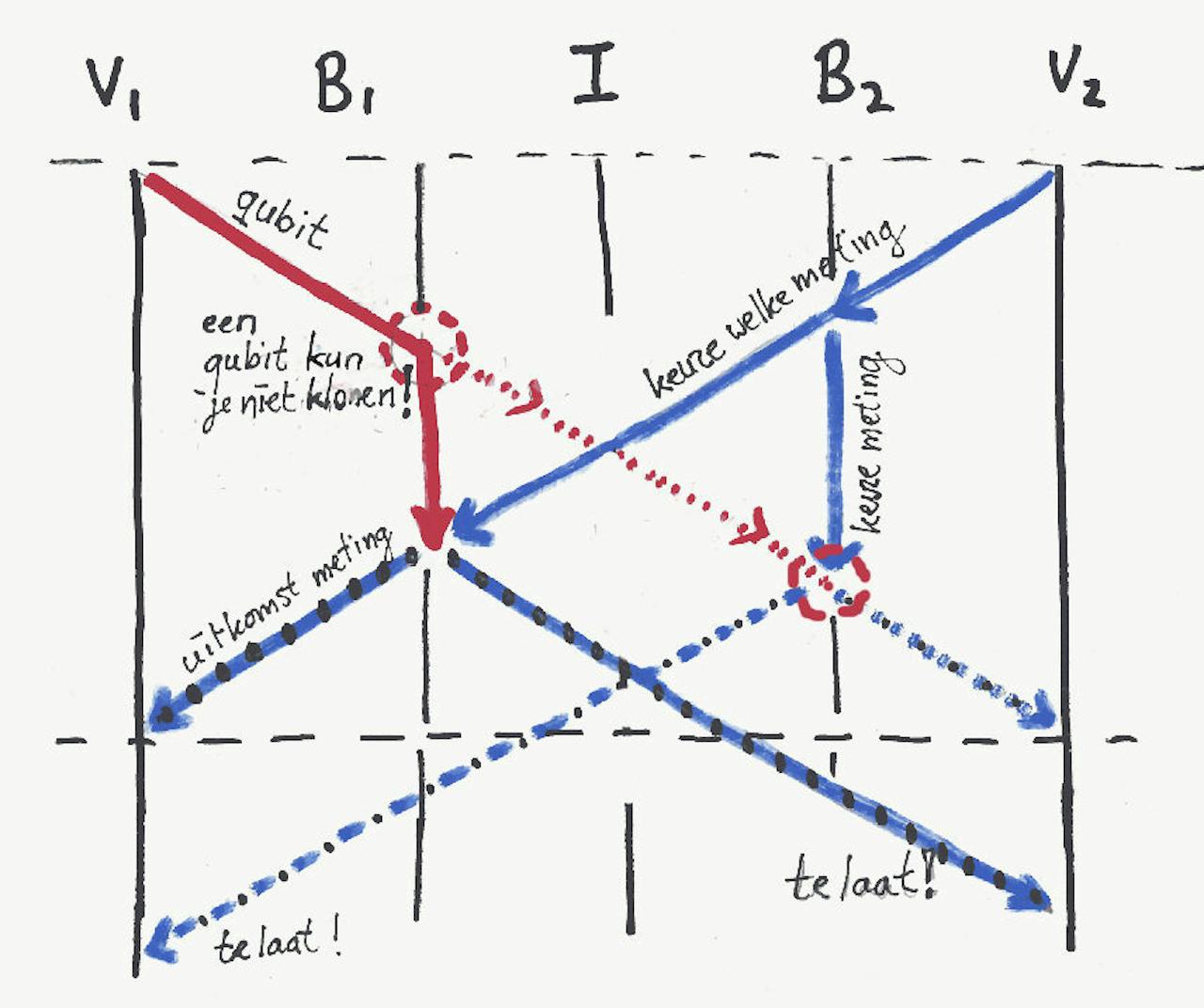
Een qubit is niet te klonen
Twee Bedriegers onderscheppen links (B1) het qubit, en rechts (B2) de keuze van de meting. Maar B1 moet kiezen of hij het qubit bewaart en wacht op B2’s bericht, óf het qubit doorstuurt naar B2. Je kunt namelijk een qubit niet zowel bewaren als doorsturen. Probeer je dat toch, dan is dat een willekeurige meting op het qubit, die meestal de verkeerde uitkomst oplevert. Kies je wel, dan krijgt of V1 of V2 de uitkomst te laat binnen.
Rood is een quantumsignaal, blauw een klassiek signaal.

 aj
Qubits meten

Een bit is de eenheid van informatie, meestal weergegeven als 0 of 1, al naar gelang de waarde die hij heeft. Een qubit is de eenheid van quantum-informatie, maar die heeft niet óf de waarde 0, óf de waarde 1, maar is in het algemeen een superpositie van beide waarden. Wat is een superpositie? Strikt genomen is dat alleen te begrijpen via de wiskunde van de quantumtheorie, maar een fysisch voorbeeld geeft een idee van wat het is.Fysiek kan een qubit een los deeltje zijn, bijvoorbeeld een elektron, of een foton (lichtdeeltje). Gaan we uit van een foton, dan wordt het qubit bepaald door de polarisatie van het foton. Licht is ook te beschouwen als een golfverschijnsel, en die golf trilt in een zekere richting loodrecht op de richting waarin het foton reist: de polarisatie. Een bekende toepassing is de polaroid zonnebril, die fotonen uit het zonlicht wegfiltert waarvan de trilling loodrecht staat op de polarisatie van het brillenglas.

Maar vooraf is die waarde nog onbepaald. Het foton had vooraf in het algemeen een polarisatie die een superpositie was van ‘evenwijdig’ en ‘loodrecht’, (zie de twee componenten van de pijl in de tekening) en die bepaalt de kans dat het foton door het brillenglas heen gaat. Maar uiteraard hangen de kansen op uitkomst 0 of 1 ook af van de stand van het brillenglas, dus van welke meting je doet.

Samenvattend: de polarisatie van een foton vóór meting is een superpositie van twee toestanden, na de meting is een van beide toestanden (0 of 1) gerealiseerd, met een kans die afhangt van welke meting je doet. Daarna bestaat de superpositie niet meer. Het qubit is dan een bit geworden.

De polarisatie van het foton kan elke stand hebben ten opzichte van het polaroid glas, net als de wijzer van een klok. Maar het foton gaat ofwel in zijn geheel door het glas heen, ofwel helemaal niet. Anders gezegd: de uitkomst is altijd of 1 (polarisatie evenwijdig aan die van het het glas) of 0 (polarisatie loodrecht op die van het glas).
Het moment dat het foton het glas raakt kun je zien als een meting van de polarisatie van het foton, uitgevoerd door het brillenglas, met als uitkomst 0 of 1.

Absurde consequenties

Helaas, dankzij diezelfde quantumtheorie en een beroemde ingeving van diezelfde Einstein is het kloonverbod te omzeilen. Hoewel hij zelf een van de grondleggers was, is Einstein nooit tevreden geweest met de quantumtheorie. Om te laten zien welke absurde consequenties die had, bedacht hij samen met de fysici Podolski en Rosen rond 1930 een experiment met EPR-paren. Als twee deeltjes, zeg fotonen, samen ontstaan, zijn ze volgens de quantumtheorie ‘verstrengeld’. De helften van zo’n EPR-paar hebben eigenlijk geen individuele eigenschappen. Zodra je een meting doet op één van beide deeltjes, veranderen ogenblikkelijk de mogelijke uitkomsten van een meting aan het andere deeltje, ook als dat inmiddels naar een ander sterrenstelsel gereisd is.

Hoewel Einstein dat niet kon geloven en het ook niet meer meegemaakt heeft, bestaan EPR-paren wel degelijk. Ze worden bijvoorbeeld gemaakt en gemanipuleerd in het Kavli Instituut van de TU Delft. Als B1 en B2 vooraf ieder beschikken over één helft van een EPR-paar, en B1 brengt zijn helft in contact met het qubit dat V1 verstuurt, dan wordt de quantumtoestand van het qubit onmiddellijk geteleporteerd naar de helft van B2. Weliswaar kan B1 dan geen meting op het qubit meer uitvoeren (het kloonverbod geldt nog steeds) maar dat hoeft ook niet: B2 kan meteen de keuze van de meting die hij onderschept van V2, uitvoeren op het geteleporteerde qubit en de uitkomst nog op tijd naar V2 én V1 sturen.

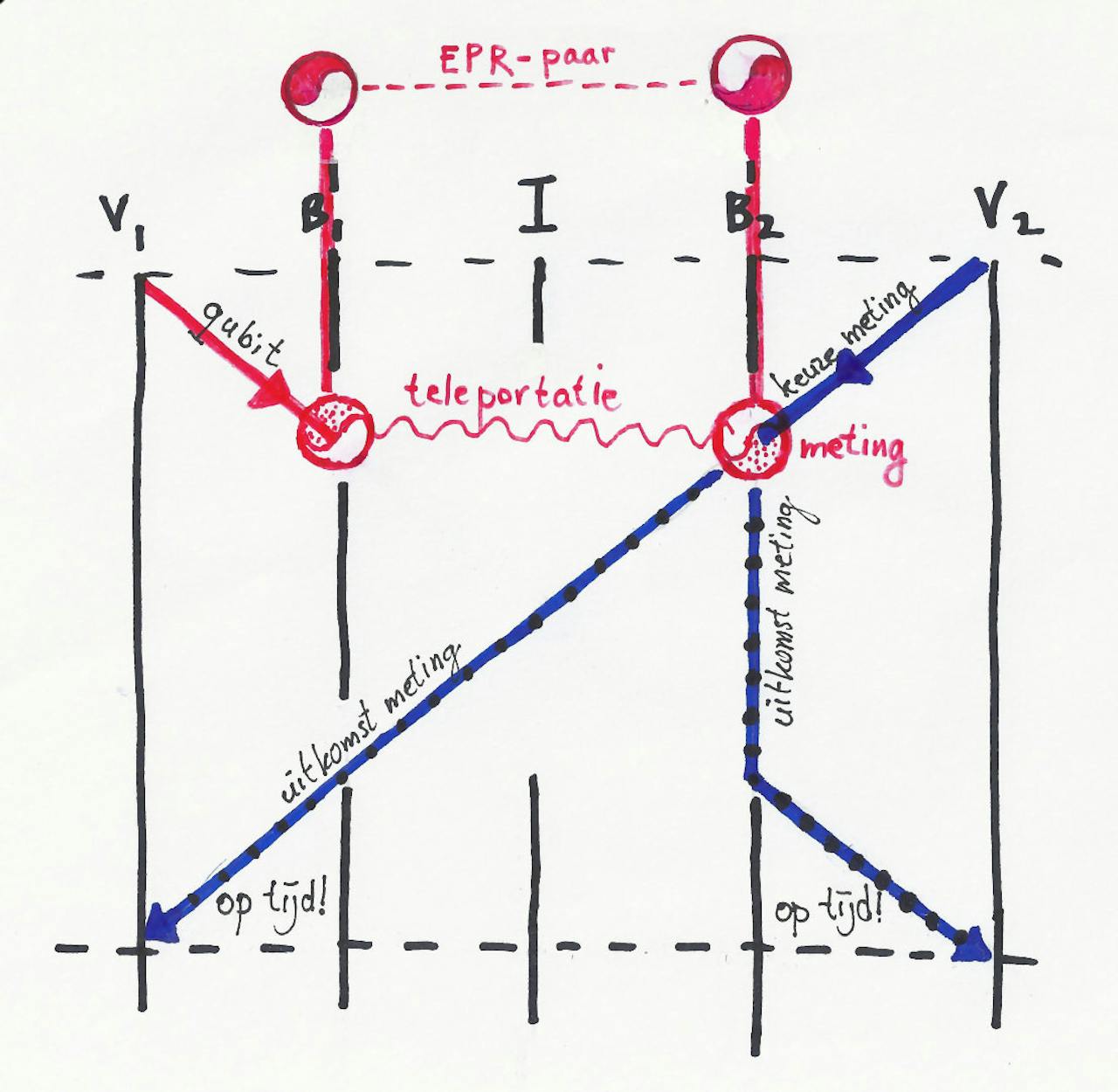
Als twee Bedriegers van te voren twee verstrengelde qubits (een EPR-paar) kunnen creëren, kan B1 de quantumtoestand van het qubit dat V1 verzendt teleporteren naar B2, die vervolgens de uitkomst van de meting nog op tijd naar V1 en V2 kan sturen. Teleporteren gebeurt onmiddellijk, en omzeilt daardoor de beperking van de lichtsnelheid. Dit is wel een sterk versimpelde voorstelling van zaken; in feite is de uitkomst van het teleportatie-experiment mede van toeval afhankelijk. Hoeveel EPR-paren in concrete situaties nodig zijn om de quantumtoestand goed over te brengen en het systeem te hacken is wat Buhrman en zijn collega’s nog aan het onderzoeken zijn.

 aj

No-go theorema

In 2010 bewezen Buhrman en zijn collega’s Nishanth Chandran, Serge Fehr, Ran Gelles, Vipul Goyal, Rafail Ostrovsky en Christian Schaffner dat je met voldoende veel EPR-paren en teleportatie elke vorm van plaatsgebonden cryptografie kunt hacken, ongeacht hoeveel qubits de Verifieerders ook oversturen en hoe ingewikkeld die het protocol ook maken. Dit universele no-go theorema bracht echter goed én slecht nieuws. Het slechte nieuws is dat absolute, onvoorwaardelijke veiligheid voor plaatsgebonden cryptografie niet bestaat. Maar iets kan principieel onmogelijk zijn, terwijl het praktisch wel degelijk mogelijk is, en dat is het goede nieuws.

Buhrman: “We vermoeden dat je een protocol kunt maken, waarbij je 300 qubits verstuurt en dan 2300 EPR-paren nodig hebt om het systeem te kraken. Maar het is hartstikke lastig om te bewijzen dat je zoveel EPR-paren nodig hebt.” Dat bewijs is nodig, omdat cryptografen heel radicaal zijn in de eisen die ze stellen aan de veiligheid van een crypto-systeem. Een EPR-paar versturen en dan één qubit teleporteren is tegenwoordig nog een technologisch hoogstandje. Maar wellicht ligt over twintig jaar een compleet glasvezelnetwerk over de wereld dat niets anders doet dan miljarden EPR-paren tussen de knooppunten heen en weer sturen.

En alleen maar een sterk vermoeden dat je heel veel EPR-paren nodig heb om een quantumprotocol te hacken is niet voldoende; dan kun je niet uitsluiten dat een genie nog eens een methode vindt om het met maar een paar dozijn exemplaren te doen. Buhrman: “Pas als bewezen is dat er meer EPR-paren nodig zijn dan deeltjes in het heelal, hebben we een veilig systeem.” Vandaar dat hij het aantal van 300 qubits als voorbeeld gaf, want 2300 (een 2 met 90 nullen erachter) is een getal dat vrijwel zeker het aantal deeltjes in het zichtbare heelal overtreft, maar ook weer niet nodeloos veel groter is dan dat aantal.

Als je eenmaal een methode hebt om praktisch volmaakt veilig iemands locatie vast te stellen, kun je een ander, al eerder in de praktijk getest, quantumprotocol gebruiken om met die persoon een sleutel uit te wisselen waarvan je zeker weet dat die niet onderweg is afgeluisterd. En met die sleutel kun je dan weer een geheimschrift opzetten waarmee je praktisch volmaakt veilig met elkaar communiceert.

Buhrman werkt momenteel samen met een onderzoeksgroep in Genève om zo’n systeem werkelijk te bouwen. De benodigde technologie is in principe beschikbaar. Technisch zijn de Verifieerders trouwens sterk in het voordeel ten opzichte van de Bedriegers. Het versturen van qubits per glasvezel is tegenwoordig namelijk goed te doen. EPR-paren manipuleren zit echter aan de grens van wat nu mogelijk is. Buhrman: “De eerlijke spelers hebben geen verstrengelde EPR-paren nodig, alleen de krakers.”

ReactiesReageer