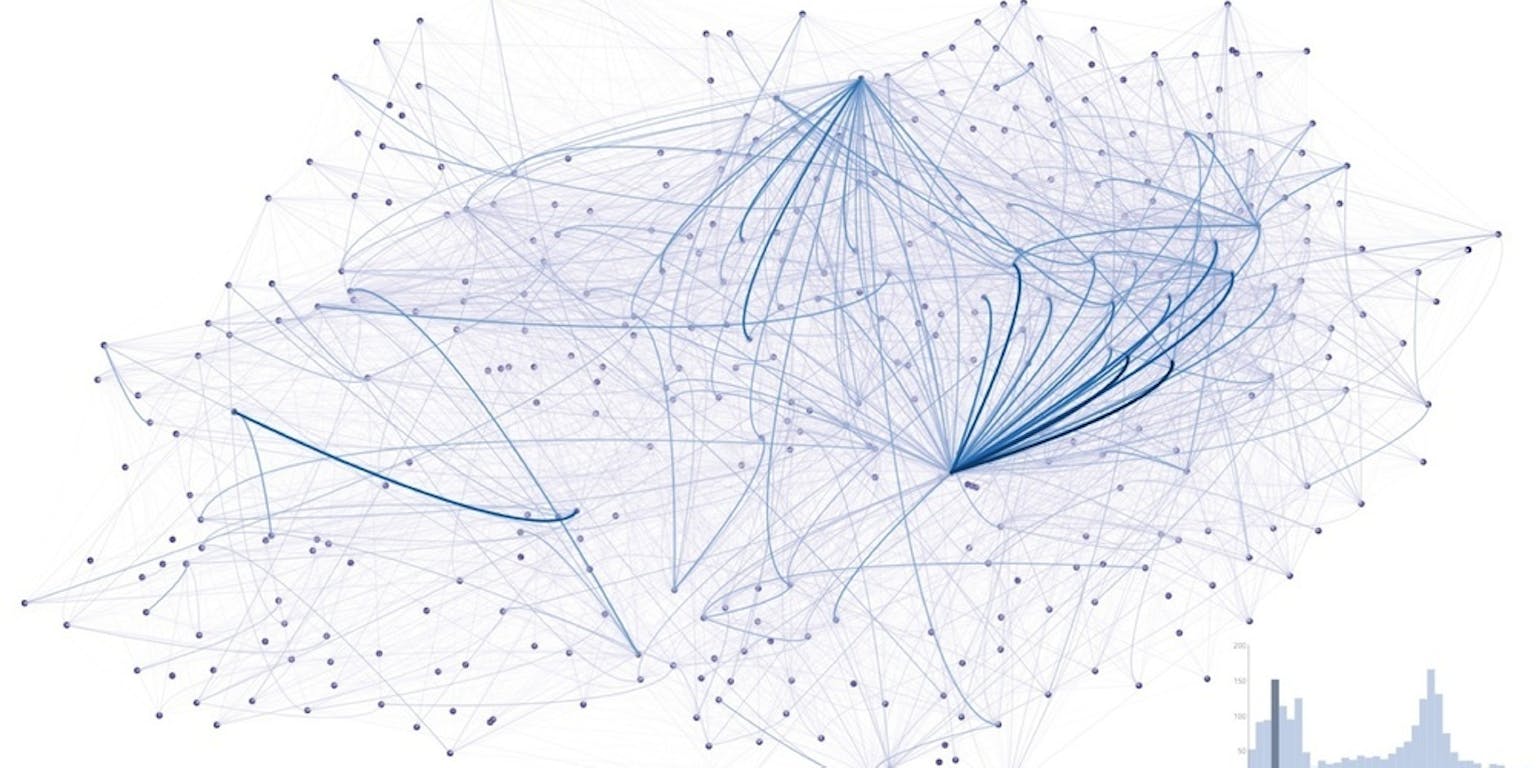
Met mijn onderzoeksbeurs ben ik vorig jaar terechtgekomen in het giCentre in Londen. Hier doen ze onderzoek naar hoe we data om kunnen zetten in handige plaatjes en grafieken, om ze makkelijker te analyseren. Zo kan je de rekenkracht van een computer combineren met de intuïtie en ervaring van de mens.
Een voorbeeldje. In Londen is er een OV-fiets (officieel Santander cycles, maar meestal worden ze de Boris bikes genoemd). Van elke reis wordt de begin- en eindlocatie en tijd vastgelegd. Maar hoe ontdek je makkelijk waar veel reizen heen gaan? Een gigantische tabel met al deze gegevens gaat je niet echt helpen hierbij. Maar als we het laten zien op een “kaart” zoals hieronder, dan vallen meteen een paar drukke routes op.
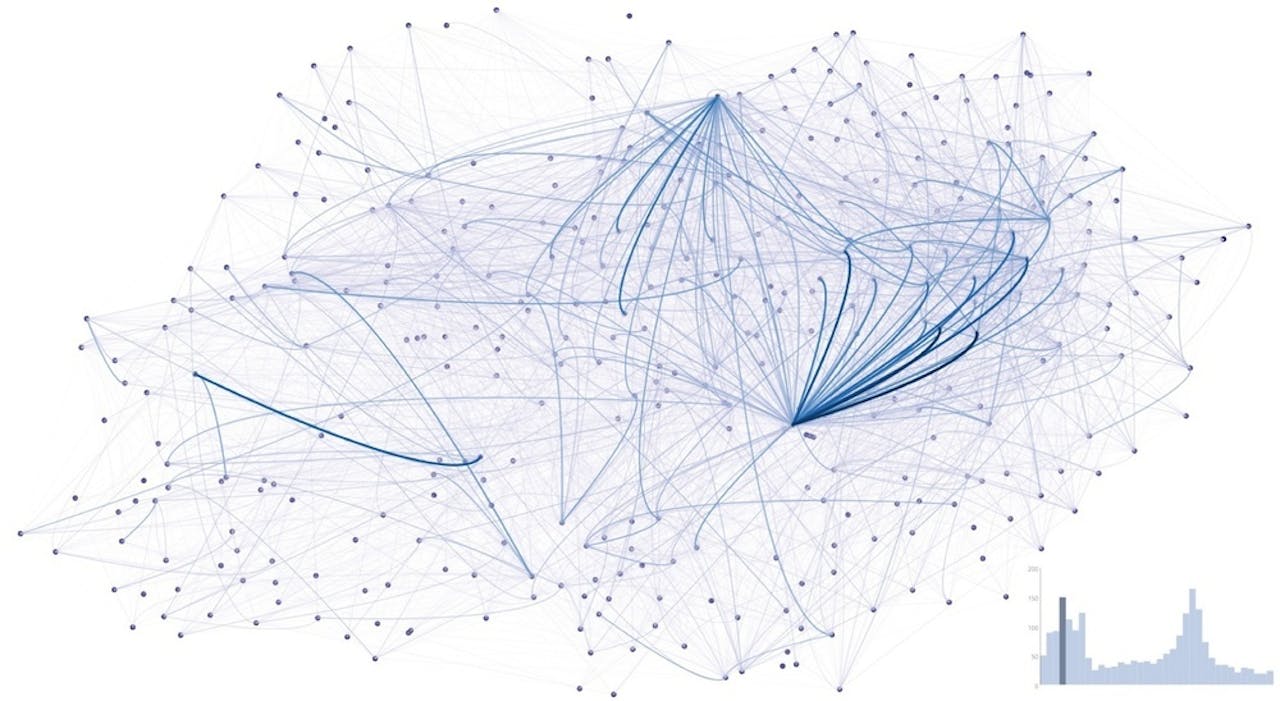
Elke punt stelt een plaats voor waar je een Boris bike kan ophalen of wegzetten. De lijnen tussen de punten stellen reizen voor, hoe dikker en donkerder de lijn, des te meer reizen zijn er gemaakt. De twee duidelijkste drukke punten zijn King’s Cross in het noorden en Waterloo Station in het midden: hier komen veel forensen binnen in Londen en gebruiken de fiets voor het laatste stuk van hun reis.
giCentre voor NEMO KennislinkEen computer kan dit natuurlijk ook berekenen, maar als je niet precies weet naar welk patroon je op zoek bent, dan is dit nog niet zo simpel. Als je meer wilt weten over deze data, is er een mooie TEDx talk van prof. Jo Wood van het giCentre hierover:
.
Schematiseren tot het uiterste
Tijdens mijn PhD deed ik onderzoek naar schematisering: hoe berekent een computer een vorm met maar een paar lijnen van, bijvoorbeeld, Nederland, zodat deze nog steeds herkenbaar is. Deze gebruik je dan bijvoorbeeld om informatie op weer te geven, zonder dat de precieze geografie afleidt of de informatie verbergt: je richt je op waar het echt om gaat, zoals bijvoorbeeld met de treinkaart van de NS – het gaat erom dat je je weg vindt, niet om waar Amsterdam precies ligt.
Als je gegevens wilt analyseren, ben je ook niet altijd geïnteresseerd in de precieze geografie, en door minder geografie te laten zien, kunnen we de overige informatie juist verduidelijken. Hier in Londen onderzoek ik dan ook wat er nu echt nodig is om nog een hint van geografie te behouden. Hiervoor pak ik een extreme vorm van schematiseren: elk gebied, is nog maar een simpel vierkantje en allemaal even groot. Je kan ook de grootte juist betekenis geven, zoals wordt uitgelegd hier.
Het handige hiervan is, is dat je allerlei informatie in dat vierkantje kan plaatsen: lijnen, grafiekjes, kleuren, tekst… Maar ja, daar staat tegen over dat je een hoop weggooit van de geografie. Maar is dat nu zo erg? In veel situaties niet. Je bent meer geïnteresseerd in of er een grof patroon is: “’s ochtends pakken mensen vooral een Boris bike van buiten het centrum naar het centrum toe”. Zeker als data-analyst, weet je waar je naar welke soort data je aan het kijken bent, en hier is herkenbaarheid minder essentieel. Maar toch willen we waar mogelijk de geografie behouden, zodat je geen verkeerde conclusies trekt, of mogelijke patronen mist.
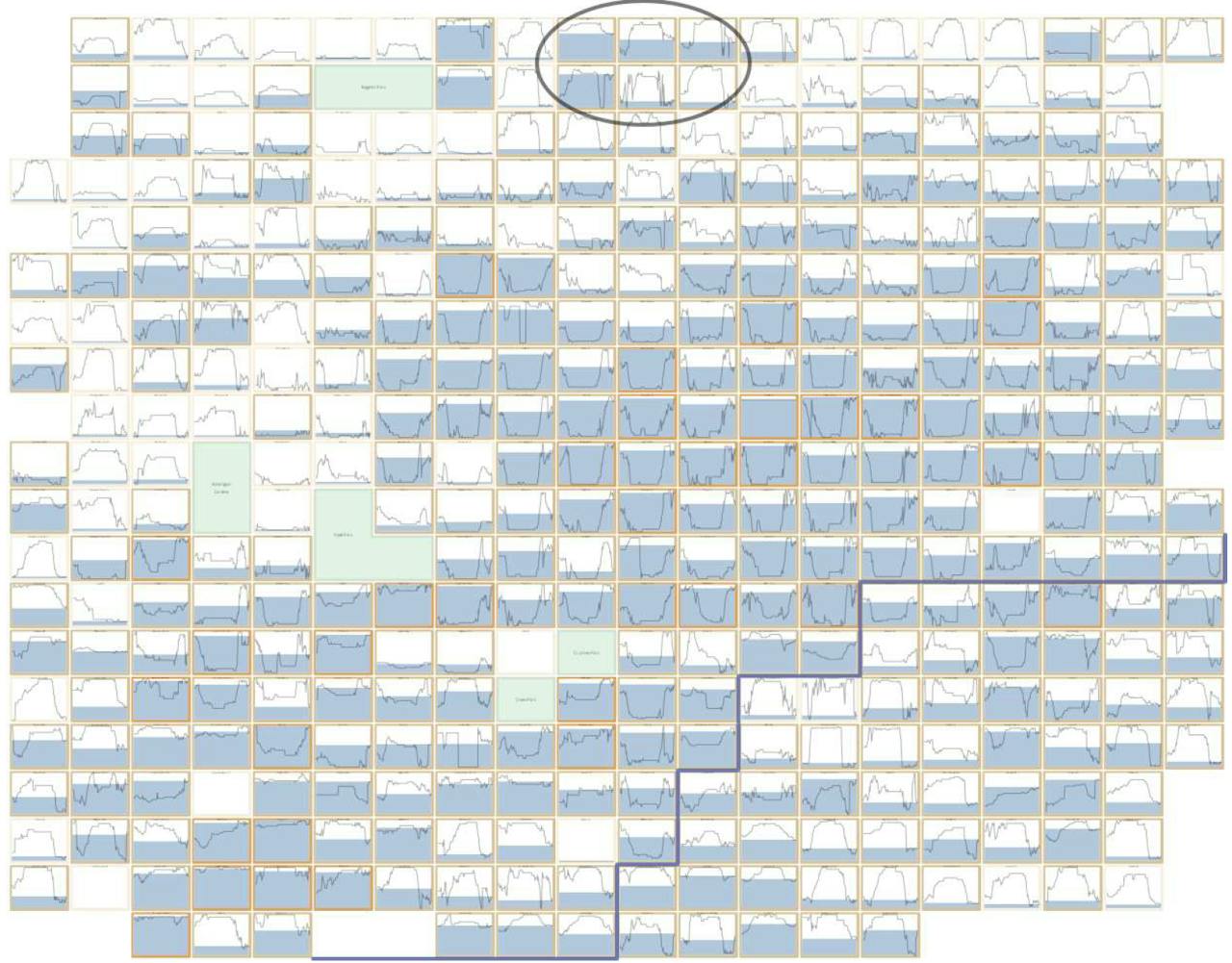
De punten van het vorige plaatje zijn vervangen door een rechthoek en zijn zo geplaatst dat je ze allemaal kunt zien, maar dat ze ook ongeveer de geografie van Londen volgen. Elke rechthoek wordt gebruikt om informatie van het “Boris bike” station te laten zien.
Puzzelen
Door de vierkantjes op een goede manier te organiseren, behoud je toch een hoop geografie. Bijvoorbeeld de afstand tussen twee gebieden, of dat de vierkantjes van twee aangrenzende gebieden netjes naast elkaar blijven, of misschien dat juist de algehele vorm behouden blijft. Neem Londen, met de 33 “Boroughs” (wijken): de plaatjes geven slechts twee voorbeelden van hoe je deze kan rangschikken. De tweede gebruikt zelfs een combinatie van eigenschappen om het beste resultaat te behalen. Deze is gebaseerd op een handmatig-gemaakte layout van AfterTheFlood en met ons werk hebben we vastgesteld dat deze een combinatie van eigenschappen gebruikt om het beste resultaat te krijgen. Het lukt nooit om dit perfect te doen met vierkantjes, maar met wat wiskunde en algoritmen kunnen we allerlei manieren berekenen om de vierkantjes in elkaar te puzzelen tot een goed geheel. De vraag blijft natuurlijk: hoe goed doen we het?
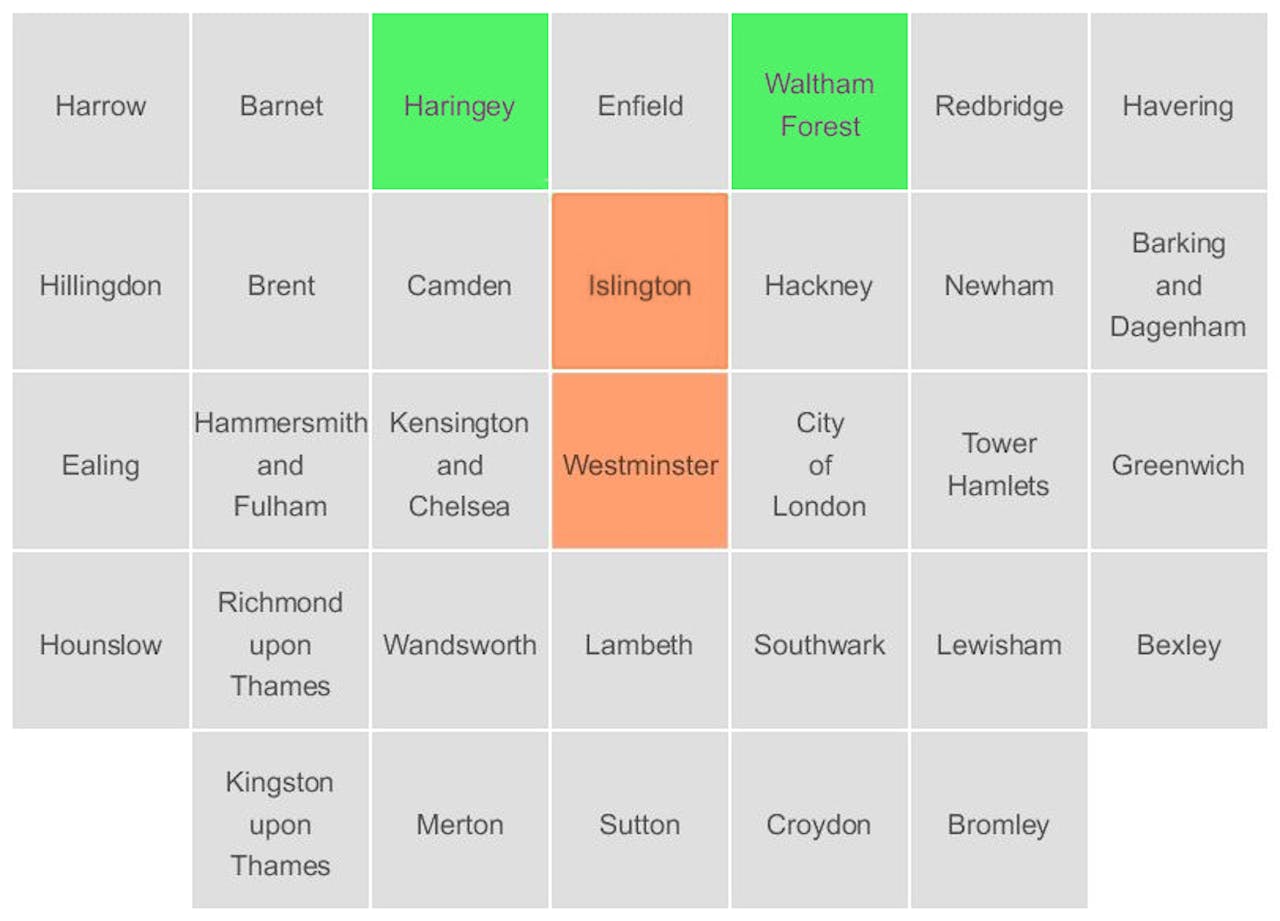
De boroughs zijn hier geplaatst naar hoe goed ze op hun plek blijven ten opzichte van een geografische kaart. Harengey en Waltham Forest liggen uit elkaar, terwijl ze in werkelijkheid aan elkaar grenzen (groen): Islington en Westminster zijn hier aangrenzend terwijl ze dat in werkelijkheid niet zijn (rood).
AftertheFlood/bewerking: Wouter Meulemans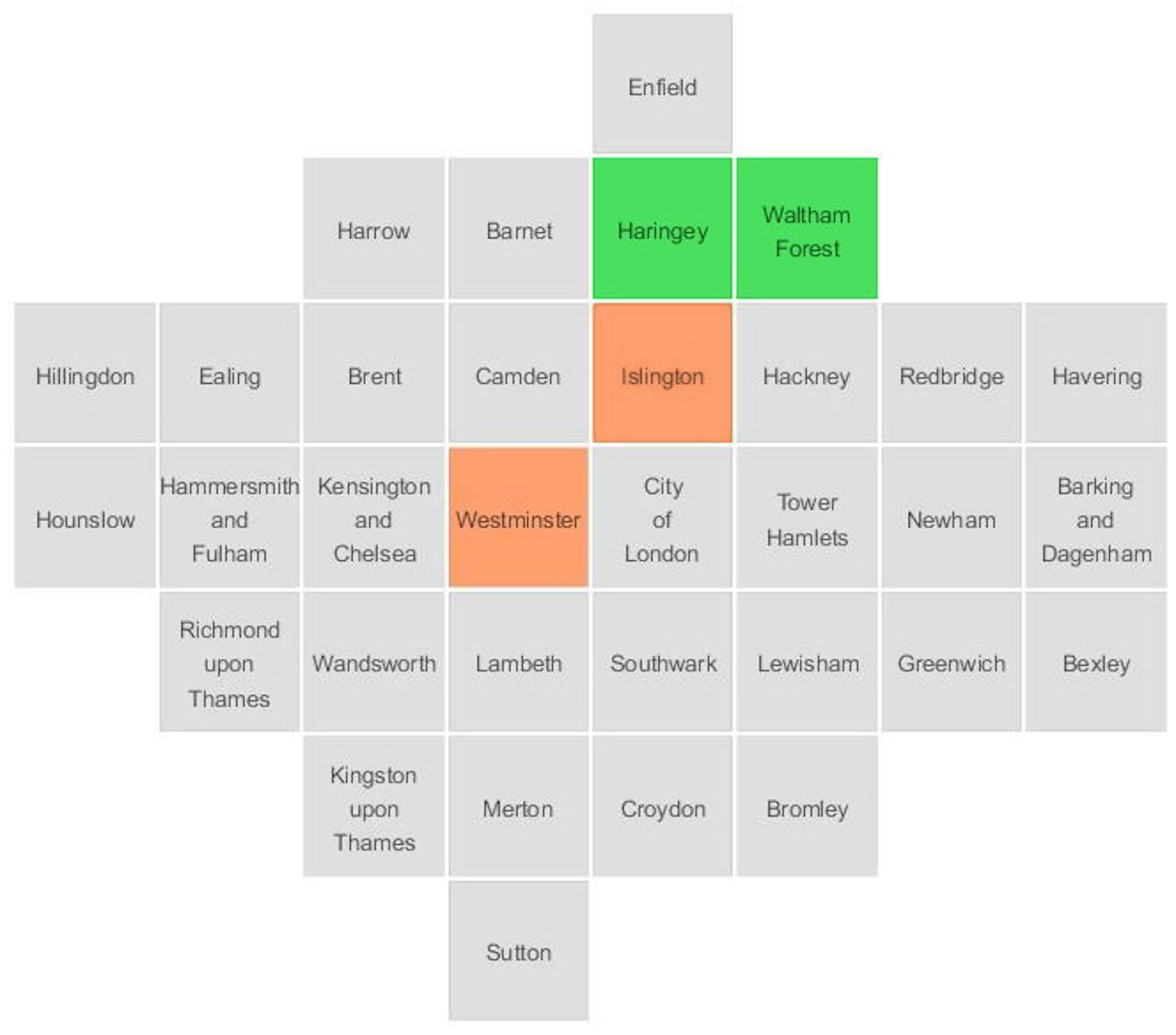
De boroughs zijn hier geplaatst naar een combinatie van topologie (het behouden van de juiste grenzen), vorm van Londen en verplaatsing. Er zijn meer lege ruimtes bij deze oplossing, waardoor de vierkantjes kleiner worden: informatie die we in de vierkantjes plaatsen is moeilijker te lezen, maar de geografie is nauwkeuriger.
AftertheFlood/bewerking: Wouter MeulemansAls we het geheel aan vierkantjes bekijken, is het meteen duidelijk dat het niet een geografisch-nauwkeurige kaart is. Maar hoe nauwkeurig is het nu? Om de juiste conclusies te trekken, is het belangrijk om een idee te krijgen van de vorming die onze vierkantjes veroorzaken. De berekeningen voor de rangschikking geven ons meteen een berg getallen die hier een hint voor geeft mogelijk maakt, maar kunnen we dit ook zichtbaar maken zodat het begrijpelijk blijft? Bijvoorbeeld door allerlei lijnen toe te voegen om afwijkingen te laten zien tussen gebieden die naast elkaar zouden moeten liggen, of de verplaatsing vanaf de geografische locatie, zoals de plaatjes hieronder aangeven.
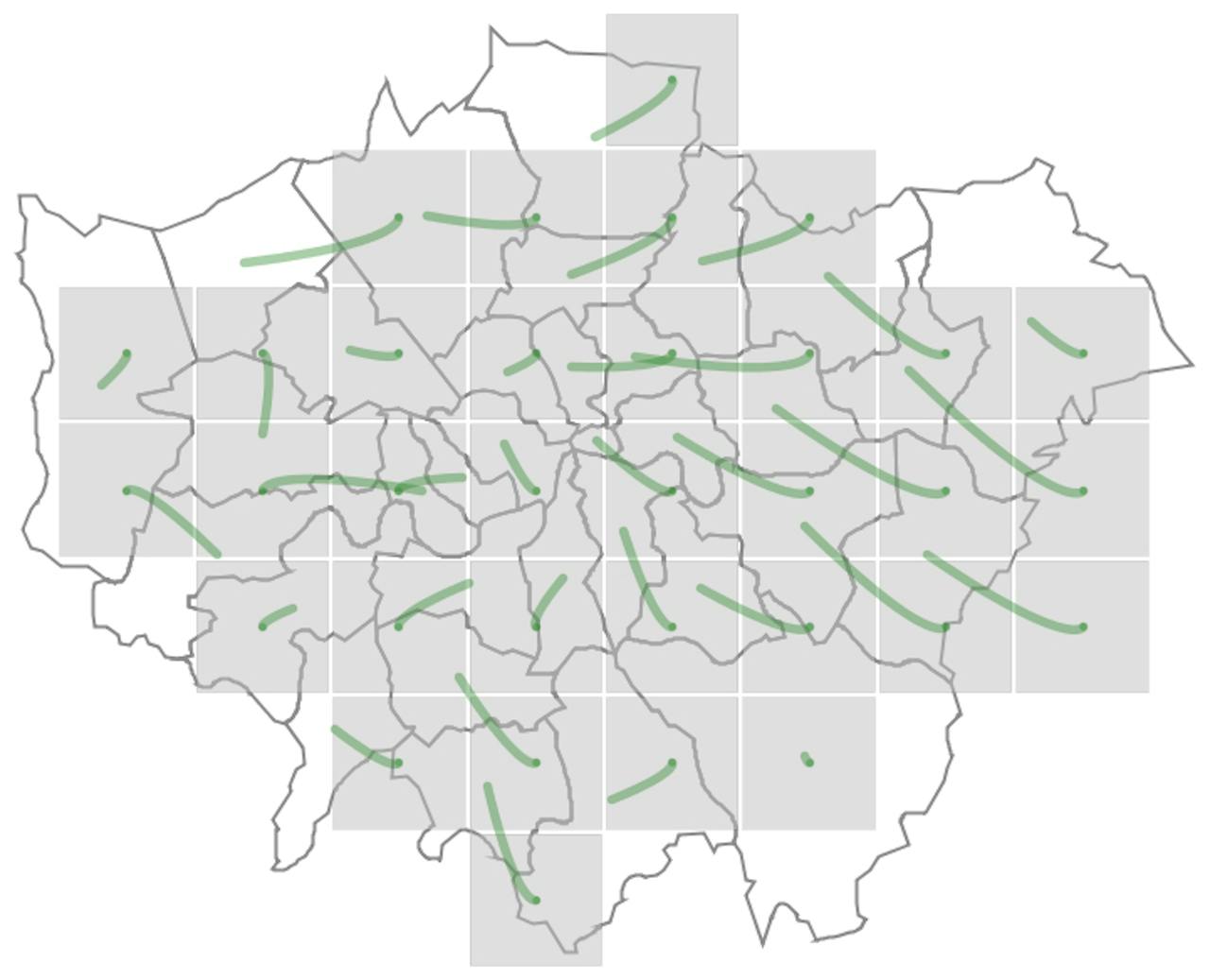
De lijnen geven aan waar elk vierkantje vandaan komt in de geografische kaart. Hoe korter de lijntjes, hoe beter!
privearchief Wouter Meulemans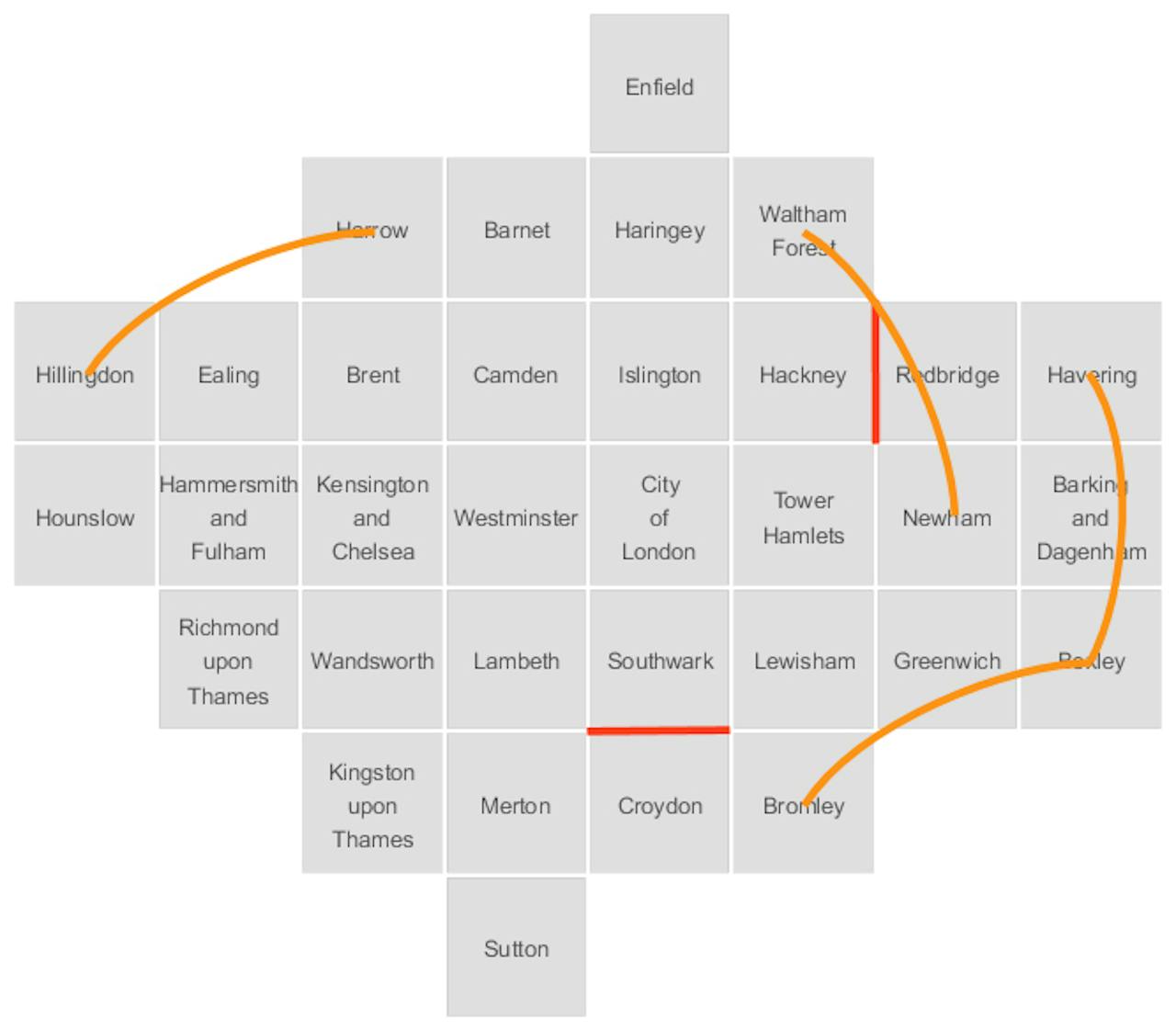
De rode lijnen geven aan waar twee vierkantjes naast elkaar liggen terwijl de gebieden die de vierkantjes weergeven geografisch niet naast elkaar horen.
privearchief Wouter MeulemansMaar misschien is een animatie nog wel effectiever? Als je dit op een simpele manier doet, kan het zijn dat het resultaat niet te volgen is. Maar door de animatie op te splitsen, of door juist een goede, soepele transformatie te berekenen, wordt dit al een stuk duidelijker. Maar hoe effectief is dit, ten opzichte van niet-bewegende plaatjes zoals hierboven? Dit is één van de vragen waar ik me momenteel mee bezig houd.
Verandering
Bij het ontwerp en gebruik van visualisaties draait het om keuzes: wat is belangrijk voor de data, welke vraag wil je beantwoorden, waar wil je nadruk op leggen, wie moet de visualisatie uiteindelijk gebruiken? Er is dus niet één correct antwoord: om dit helemaal uit te pluizen, is meer tijd nodig dan ik hier in Londen heb en mijn tijd hier zit er al weer bijna op. Dit is dan ook meteen mijn laatste blog als “Face of Science”. Ik hoop dat ik een aantal interessante blogs heb kunnen schrijven. Mocht je geïnteresseerd zijn in algoritmiek, visualisatie, of de combinatie hiervan, neem gerust contact op. Vanaf november ben ik weer te vinden bij de Technische Universiteit Eindhoven, maar nu als universitair docent: weer een volgende stap!